Bài 4 trang 68 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các ứng dụng của hàm số bậc nhất. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về hàm số, cách xác định hệ số góc và tung độ gốc, cũng như khả năng áp dụng vào giải quyết các vấn đề cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 68 sách bài tập Toán 8 - Chân trời sáng tạo tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
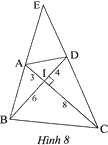
Trong Hình 8, cho tam giác BEC $\left( BE<EC \right)$. Cho biết $AC\bot BD,$ chứng minh rằng:
Đề bài
Trong Hình 8, cho tam giác BEC $\left( BE<EC \right)$. Cho biết $AC\bot BD,$ chứng minh rằng:
a) $\Delta AIB\backsim \Delta DIC$.
b) $EA.EB=EC.ED$.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông: Nếu tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải chi tiết
a) Tam giác AIB và tam giác DIC có: $\widehat{AIB}=\widehat{DIC}={{90}^{0}},\frac{AI}{ID}=\frac{IB}{IC}\left( =\frac{3}{4} \right)$
Do đó, $\Delta AIB\backsim \Delta DIC\left( c.g.c \right)$
b) Vì $\Delta AIB\backsim \Delta DIC\left( cmt \right)$ nên $\widehat{ABI}=\widehat{DCI}$
Tam giác EAC và tam giác EDB có: $\widehat{EBD}=\widehat{ACE}\left( cmt \right),\widehat{E}\ chung$
Do đó, \(\Delta EAC\backsim \Delta EDB\left( g.g \right)\), suy ra $\frac{EA}{ED}=\frac{EC}{EB}$, vậy $EA.EB=EC.ED$
Bài 4 trang 68 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc xác định hàm số bậc nhất biểu diễn mối quan hệ giữa hai đại lượng. Để giải bài toán này, chúng ta cần phân tích đề bài, xác định các yếu tố quan trọng và áp dụng các kiến thức đã học về hàm số bậc nhất.
Trước khi bắt đầu giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 4 trang 68, đề bài thường cung cấp một tình huống thực tế và yêu cầu học sinh xác định hàm số bậc nhất biểu diễn mối quan hệ giữa hai đại lượng trong tình huống đó. Ví dụ, đề bài có thể cho biết vận tốc của một vật thể thay đổi như thế nào theo thời gian, hoặc chi phí sản xuất một sản phẩm phụ thuộc vào số lượng sản phẩm được sản xuất.
Hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc. Để xác định hàm số bậc nhất, chúng ta cần tìm giá trị của a và b. Có nhiều phương pháp để tìm a và b, tùy thuộc vào thông tin được cung cấp trong đề bài. Một số phương pháp phổ biến bao gồm:
Giả sử đề bài yêu cầu xác định hàm số bậc nhất biểu diễn mối quan hệ giữa quãng đường đi được (y) của một ô tô và thời gian di chuyển (x). Biết rằng ô tô đi với vận tốc không đổi là 60 km/h và ban đầu ô tô cách điểm xuất phát 10 km.
Lời giải:
Vậy hàm số bậc nhất biểu diễn mối quan hệ giữa quãng đường đi được và thời gian di chuyển của ô tô là y = 60x + 10.
Khi giải bài tập về hàm số bậc nhất, các em học sinh cần lưu ý những điều sau:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về hàm số bậc nhất, các em học sinh có thể làm thêm các bài tập sau:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ hiểu rõ hơn về bài 4 trang 68 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 và tự tin giải các bài tập tương tự.