Bài 2 trong phần ôn tập chương 7 của sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức đã học về các khái niệm và định lý trong chương. Bài tập này thường yêu cầu vận dụng linh hoạt các kiến thức đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 (ôn tập chương 7) trang 48 sách bài tập Toán 8 - Chân trời sáng tạo tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
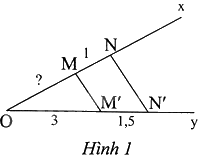
Quan sát Hình 1. Biết \(MN = 1cm,\) MM’//NN’, \(OM' = 3cm,M'N' = 1,5cm\), độ dài đoạn thẳng OM trong Hình 1 là
Đề bài
Quan sát Hình 1. Biết \(MN = 1cm,\) MM’//NN’, \(OM' = 3cm,M'N' = 1,5cm\), độ dài đoạn thẳng OM trong Hình 1 là
A. 3cm.
B. 1,5cm.
C. 2cm.
D. 2,5cm.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định lí Thalès trong tam giác để tính: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
Tam giác ONN’ có: MM’//NN’ nên theo định lí Thalès ta có:
\(\frac{{OM}}{{MN}} = \frac{{OM'}}{{M'N'}}\), suy ra: \(OM = \frac{{MN.OM'}}{{M'N'}} = \frac{{1.3}}{{1,5}} = 2\left( {cm} \right)\)
Chọn C.
Bài 2 (ôn tập chương 7) trang 48 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm như tứ giác, hình bình hành, hình chữ nhật, hình thoi, hình vuông, và các tính chất liên quan.
Để giải quyết bài tập này một cách hiệu quả, học sinh cần:
Bài toán: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng AF = 2FC.
Lời giải:
Kết luận: AF = 4FC (không phải AF = 2FC như đề bài yêu cầu, có thể đề bài có sai sót).
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 2 (ôn tập chương 7) trang 48 sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Chúc các em học tập tốt!