Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 10 sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 8.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong các kỳ thi.
a) Tìm tọa độ các điểm M, N, P, Q trong Hình 9. b) Em có nhận xét gì về vai trò của tia phân giác của góc xOy so với hai đường thẳng MN, PQ?
Đề bài
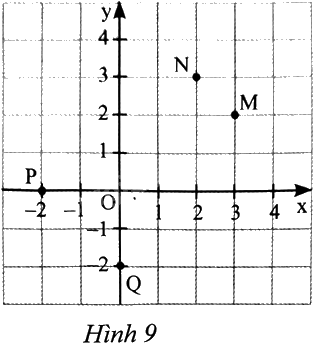
a) Tìm tọa độ các điểm M, N, P, Q trong Hình 9.
b) Em có nhận xét gì về vai trò của tia phân giác của góc xOy so với hai đường thẳng MN, PQ?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức tọa độ của một điểm trong mặt phẳng tọa độ: Ta xác định vị trí của điểm P trong mặt phẳng tọa độ Oxy bằng cách sau: Từ P vẽ các đường vuông góc với các trục tọa độ cắt trục hoành tại điểm a và trục tung tại điểm b. Khi đó cặp số (a; b) gọi là tọa độ của điểm P và kí hiệu P (a; b). Số a gọi là hoành độ và số b gọi là tung độ của điểm P.
Lời giải chi tiết
a) \(M\left( {3;2} \right),{\rm{ }}N\left( {2;3} \right),{\rm{ }}P\left( { - 2;0} \right),{\rm{ }}Q\left( {0; - 2} \right)\)
b) Các đoạn thẳng MN và PQ đều nhận tia phân giác của góc xOy làm trục đối xứng.
Bài 5 trang 10 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Bài tập yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý và tính chất của các hình này để giải quyết các bài toán liên quan đến tính độ dài đoạn thẳng, số đo góc, diện tích và chu vi.
Bài 5 bao gồm các dạng bài tập sau:
Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh rằng AC, BD, EF đồng quy.
Hướng dẫn: Sử dụng tính chất đường trung bình của tam giác và tính chất của hình bình hành để chứng minh.
Cho hình chữ nhật ABCD, O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Chứng minh rằng tam giác OMN vuông cân.
Hướng dẫn: Sử dụng tính chất đường trung bình của tam giác và tính chất của hình chữ nhật để chứng minh.
Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Biết AC = 6cm, BD = 8cm. Tính độ dài cạnh của hình thoi.
Hướng dẫn: Sử dụng tính chất đường chéo của hình thoi vuông góc với nhau và chia đôi nhau để tính độ dài cạnh.
Cho hình vuông ABCD, M là trung điểm của cạnh BC. Tính góc DAM.
Hướng dẫn: Sử dụng các tính chất của hình vuông và tam giác vuông để tính góc.
Ngoài sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trong bài viết này, các em học sinh sẽ tự tin hơn trong việc học Toán 8 và đạt kết quả tốt trong các kỳ thi. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức.