Giải bài 8 trang 65 Sách bài tập Toán 8 - Chân trời sáng tạo

Giải bài 8 trang 65 sách bài tập toán 8 - Chân trời sáng tạo

Giải bài 8 trang 65 Sách bài tập Toán 8 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 8 trang 65 sách bài tập Toán 8 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng trình bày các bước giải một cách rõ ràng và logic nhất.

Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán 8, tự tin giải các bài tập và đạt kết quả tốt trong học tập.

Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.

Đề bài

Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.

Phương pháp giải - Xem chi tiết Giải bài 8 trang 65 sách bài tập toán 8 - Chân trời sáng tạo 1

+ Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

+ Sử dụng kiến thức về dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

Lời giải chi tiết

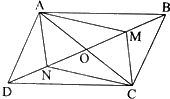
Giải bài 8 trang 65 sách bài tập toán 8 - Chân trời sáng tạo 2

Tứ giác ABCD là hình bình hành nên \(OA = OC\), \(OB = OD\)

Mà: \(ON = \frac{1}{2}OD\) (do N là trung điểm của OD)

\(OM = \frac{1}{2}OB\) (do M là trung điểm của OB)

Do đó, \(OM = ON\)

Tứ giác AMCN có: \(OM = ON\) (cmt), \(OA = OC\) (cmt) nên tứ giác AMCN là hình bình hành.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 8 trang 65 sách bài tập toán 8 - Chân trời sáng tạo đặc sắc thuộc chuyên mục giải sgk toán 8 trên toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 8 trang 65 Sách bài tập Toán 8 - Chân trời sáng tạo: Tổng quan

Bài 8 trang 65 sách bài tập Toán 8 - Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh phải hiểu rõ định nghĩa, các tính chất đặc trưng của hình thang cân, cũng như các phương pháp chứng minh một tứ giác là hình thang cân.

Nội dung chi tiết bài 8 trang 65

Bài 8 thường bao gồm các dạng bài tập sau:

Chứng minh một tứ giác là hình thang cân: Dạng bài này yêu cầu học sinh sử dụng các dấu hiệu nhận biết hình thang cân, ví dụ như chứng minh hai cạnh đáy song song và hai cạnh bên bằng nhau, hoặc chứng minh hai góc kề một cạnh bên bằng nhau.
Tính độ dài các cạnh, đường cao của hình thang cân: Dạng bài này yêu cầu học sinh vận dụng các tính chất của hình thang cân, đặc biệt là tính chất hai cạnh bên bằng nhau và hai đường chéo bằng nhau, để tính toán các yếu tố cần tìm.
Ứng dụng tính chất của hình thang cân vào giải toán thực tế: Dạng bài này thường liên quan đến các bài toán về đo đạc, tính toán trong thực tế, đòi hỏi học sinh phải biết cách chuyển đổi bài toán hình học thành bài toán số học và ngược lại.

Hướng dẫn giải chi tiết bài 8 trang 65

Để giải bài 8 trang 65 sách bài tập Toán 8 - Chân trời sáng tạo một cách hiệu quả, bạn cần:

Nắm vững định nghĩa và các tính chất của hình thang cân: Đây là nền tảng cơ bản để giải quyết mọi bài toán liên quan đến hình thang cân.
Đọc kỹ đề bài và xác định yêu cầu: Điều này giúp bạn tránh sai sót và lựa chọn phương pháp giải phù hợp.
Vẽ hình minh họa: Việc vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán và tìm ra các mối liên hệ giữa các yếu tố.
Sử dụng các công cụ hỗ trợ: Bạn có thể sử dụng thước kẻ, compa, eke để vẽ hình và đo đạc các yếu tố.
Kiểm tra lại kết quả: Sau khi giải xong bài toán, bạn nên kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví dụ minh họa giải bài 8 trang 65

Bài toán: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = 6cm. Tính độ dài đường cao của hình thang.

Giải:

Kẻ AH và BK vuông góc với CD (H, K thuộc CD).
Ta có: HK = AB = 5cm.
Suy ra: DH = KC = (CD - HK) / 2 = (10 - 5) / 2 = 2.5cm.
Áp dụng định lý Pitago vào tam giác ADH vuông tại H, ta có: AH² = AD² - DH² = 6² - 2.5² = 36 - 6.25 = 29.75.
Vậy: AH = √29.75 ≈ 5.45cm.

Kết luận: Độ dài đường cao của hình thang ABCD là khoảng 5.45cm.

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 8 - Chân trời sáng tạo, hoặc tìm kiếm trên các trang web học toán online.