Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 sách Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 16 trang 74, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho (BM = DN)
Đề bài
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho \(BM = DN\)
a) Chứng minh rằng tứ giác AMCN là hình bình hành.
b) Xác định vị trí của điểm M để tia AM cắt BC tại trung điểm của BC.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
b) Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết
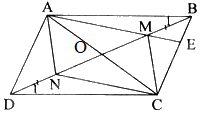
a) Vì ABCD là hình bình hành nên \(AB = CD\), AB//CD. Do đó, \(\widehat {MBA} = \widehat {NDC}\) (hai góc so le trong)
Tam giác AMB và tam giác CND có:
\(AB = CD\)(cmt), \(\widehat {MBA} = \widehat {NDC}\), \(BM = DN\) (gt)
Do đó, \(\Delta AMB = \Delta CND\left( {c - g - c} \right)\) nên \(AM = CN\)
Chứng minh tương tự ta có: \(\Delta AND = \Delta CMB\left( {c - g - c} \right)\) nên \(AN = CM\)
Tứ giác AMCN có: \(AM = CN\), \(AN = CM\) nên tứ giác AMCN là hình bình hành.
b) Gọi E là giao điểm của AM và BC, O là giao điểm của AC và BD nên O là trung điểm của AC
Để E là trung điểm của của BC thì AE là đường trung tuyến của tam giác ABC.
Lại có BO là trung tuyến của tam giác ABC.
M là giao điểm của EA và BO nên M là trọng tâm của tam giác ABC. Do đó, \(MB = \frac{2}{3}BO\)
Mà \(BO = \frac{1}{2}BD\) nên \(MB = \frac{1}{2}.\frac{2}{3}BD = \frac{1}{3}BD\)
Vậy khi M nằm trên đoạn thẳng BD sao cho \(MB = \frac{1}{3}BD\) thì tia AM cắt BC tại trung điểm của BC.
Bài 16 trang 74 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học về các hình khối trong không gian, cụ thể là hình lăng trụ đứng và hình chóp. Bài tập này thường yêu cầu học sinh vận dụng các công thức tính diện tích xung quanh, diện tích đáy, thể tích của các hình này để giải quyết các bài toán thực tế.
Bài 16 thường bao gồm các dạng bài tập sau:
Để giải bài 16 trang 74 hiệu quả, bạn cần nắm vững các kiến thức sau:
Ví dụ: Cho hình lăng trụ đứng có đáy là hình vuông cạnh 5cm, chiều cao 8cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ.
Giải:
Để giải các bài tập về hình học không gian một cách hiệu quả, bạn nên:
Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 16 trang 74 sách bài tập Toán 8 Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao!