Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 16 trang 27 sách bài tập Toán 8 Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải cụ thể, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Ở hình bên, độ dài các cạnh AB, BC và GH được cho theo a và b; hai cạnh CD và EF bằng nhau; ba cạnh AH, GF và ED bằng nhau.
Đề bài
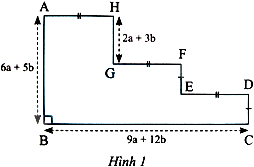
Ở hình bên, độ dài các cạnh AB, BC và GH được cho theo a và b; hai cạnh CD và EF bằng nhau; ba cạnh AH, GF và ED bằng nhau.
a) Tìm độ dài các cạnh AH, GF, ED.
b) Tìm độ dài các cạnh CD, EF.
c) Tính chu vi của hình bên.
Phương pháp giải - Xem chi tiết
- Sử dụng kiến thức chia hai phân thức để tính: Muốn chia phân thức \(\frac{A}{B}\) cho phân thức \(\frac{C}{D}\) (C khác đa thức không), ta nhân phân thức \(\frac{A}{B}\) với phân thức \(\frac{D}{C}\): \(\frac{A}{B}:\frac{C}{D} = \frac{A}{B}.\frac{D}{C}\)
- Sử dụng kiến thức cộng trừ hai đa thức để tính:
+ Viết hai đa thức trong ngoặc nối với nhau bằng dấu cộng (+) hay trừ (–).
+ Bỏ dấu ngoặc rồi thu gọn đa thức thu được.
Lời giải chi tiết
a) Ta có: \(AH = GF = ED = \frac{{BC}}{3} = \frac{{9a + 12b}}{3} = \frac{{3\left( {3a + 4b} \right)}}{3} = 3a + 4b\);
b) Ta có: \(CD = FE = \frac{{AB - GH}}{2} = \frac{{\left( {6a + 5b} \right) - \left( {2a + 3b} \right)}}{2} = \frac{{4a + 2b}}{2} = \frac{{2\left( {2a + b} \right)}}{2} = 2a + b\)
c) Chu vi của hình trên là:
\(AB + BC + CD + DE + FE + GF + GH + AH = AB + BC + AB + BC\)
\( = 6a + 5b + 9a + 12b + 9a + 12b + 6a + 5b\)
\( = \left( {6a + 6a + 9a + 9a} \right) + \left( {5b + 12b + 12b + 5b} \right) = 30a + 34b\)
Bài 16 trang 27 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Bài tập yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý và tính chất của các hình này để giải quyết các bài toán liên quan đến tính độ dài đoạn thẳng, số đo góc, diện tích và chu vi.
Bài 16 bao gồm một số câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Để giải bài 16 trang 27 sách bài tập Toán 8 Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Bài tập: Cho hình bình hành ABCD, biết AB = 5cm, BC = 3cm và góc ABC = 60 độ. Tính diện tích hình bình hành ABCD.
Giải:
Diện tích hình bình hành ABCD được tính theo công thức: S = AB * BC * sin(ABC)
Thay số, ta có: S = 5 * 3 * sin(60) = 15 * (√3/2) ≈ 12.99 cm2
Ngoài việc giải bài 16 trang 27, học sinh nên tìm hiểu thêm về:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 8 Chân trời sáng tạo hoặc trên các trang web học toán online.
Bài 16 trang 27 sách bài tập Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Việc giải bài tập này một cách chính xác và hiệu quả sẽ giúp học sinh tự tin hơn trong việc học Toán 8.
| Hình | Tính chất |
|---|---|
| Hình bình hành | Các cạnh đối song song và bằng nhau; Các góc đối bằng nhau. |
| Hình chữ nhật | Có bốn góc vuông; Các cạnh đối song song và bằng nhau; Hai đường chéo bằng nhau. |
| Hình thoi | Bốn cạnh bằng nhau; Các cạnh đối song song; Hai đường chéo vuông góc với nhau. |
| Hình vuông | Có bốn góc vuông và bốn cạnh bằng nhau; Hai đường chéo bằng nhau và vuông góc với nhau. |