Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 11 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp các bước giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các ví dụ minh họa để bạn có thể nắm vững kiến thức. Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết ngay sau đây!
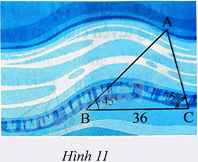
Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với \(NP = 6cm,\widehat N = {45^0},\widehat P = {75^0}\).
Đề bài
Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với \(NP = 6cm,\widehat N = {45^0},\widehat P = {75^0}\).
a) Chứng minh $\Delta MNP\backsim \Delta ABC$
b) Dùng thước đo chiều dài cạnh MP của tam giác MNP. Tính khoảng cách giữa hai điểm A và C ở hai bờ sông trong Hình 11.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g): Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
a) Tam giác MNP và tam giác ABC có: \(\widehat N = \widehat B\left( { = {{45}^0}} \right),\widehat P = \widehat C\left( { = {{75}^0}} \right)\)
Do đó, $\Delta MNP\backsim \Delta ABC\left( g.g \right)$
b) Vì $\Delta MNP\backsim \Delta ABC\left( cmt \right)$ nên \(\frac{{MP}}{{AC}} = \frac{{NP}}{{BC}}\), do đó, \(AC = \frac{{MP.BC}}{{NP}} = \frac{{MP.36}}{6} = 6MP\)
Học sinh đo độ dài đọan thẳng MP trong hình mình vẽ, từ đó tính được AC.
Bài 11 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các định lý liên quan.
Bài tập 11 yêu cầu học sinh chứng minh một số tính chất liên quan đến đường trung bình của tam giác và hình thang. Để giải bài tập này, học sinh cần:
Để giúp học sinh hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết bài tập 11 trang 64:
(Giải thích chi tiết các bước chứng minh, sử dụng các định lý và tính chất đã nêu ở trên. Ví dụ: Xét tam giác ABC, gọi M là trung điểm của AB, N là trung điểm của AC. Chứng minh MN song song với BC và MN = 1/2 BC. Sử dụng định nghĩa đường trung bình của tam giác.)
(Giải thích chi tiết các bước chứng minh, sử dụng các định lý và tính chất đã nêu ở trên. Ví dụ: Xét hình thang ABCD, gọi M là trung điểm của AD, N là trung điểm của BC. Chứng minh MN song song với AB và CD, và MN = (AB + CD)/2. Sử dụng định nghĩa đường trung bình của hình thang.)
Ngoài bài tập 11, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về đường trung bình của tam giác và hình thang. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức, bạn có thể thử giải các bài tập sau:
Bài 11 trang 64 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về đường trung bình của tam giác và hình thang. Hy vọng với lời giải chi tiết và các phương pháp giải đã trình bày, các bạn học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
| Khái niệm | Định nghĩa |
|---|---|
| Đường trung bình của tam giác | Đoạn thẳng nối trung điểm của hai cạnh. |
| Đường trung bình của hình thang | Đoạn thẳng nối trung điểm của hai cạnh bên. |