Bài 6 trang 75 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 75 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), M là điểm bất kì trên cạnh AC. Kẻ \(MD \bot BC\left( {D \in BC} \right)\).
Đề bài
Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), M là điểm bất kì trên cạnh AC. Kẻ \(MD \bot BC\left( {D \in BC} \right)\).
a) Chứng minh rằng $\Delta DMC\backsim \Delta ABC$.
b) Gọi E là giao điểm của đường thẳng AB và đường thẳng MD. Chứng minh rằng \(DB.DC = DE.DM\)
c) Đường thẳng BM cắt EC tại K. Chứng minh rằng \(\widehat {EKA} = \widehat {EBC}\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để tính: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c) để tính chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
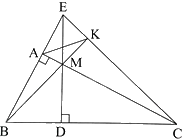
a) Tam giác DMC và tam giác ABC có:
\(\widehat {MDC} = \widehat {BAC} = {90^0},\widehat {ACB}\;chung\)
Do đó, $\Delta DMC\backsim \Delta ABC\left( g.g \right)$
b) Tam giác DBE và tam giác DMC có:
\(\widehat {BDE} = \widehat {MDC} = {90^0},\widehat {DEB} = \widehat {DCM}\) (cùng phụ với góc ABC)
Suy ra \(\Delta DBE\backsim \Delta DMC\left( g.g \right)\)
Suy ra: \(\frac{{DB}}{{DM}} = \frac{{DE}}{{DC}}\), nên \(DB.DC = DE.DM\)
c) Tam giác EBC có hai đường cao ED và CA cắt nhau tại M nên M là trực tâm của tam giác EBC. Do đó, \(BK \bot EC\)
Tam giác EAC và tam giác EKB có:
\(\widehat {EAC} = \widehat {EKB} = {90^0},\widehat {BEC}\;chung\)
Do đó, $\Delta EAC\backsim \Delta EKB\left( g.g \right)$nên \(\frac{{EA}}{{EK}} = \frac{{EC}}{{EB}}\), hay \(\frac{{EA}}{{EC}} = \frac{{EK}}{{EB}}\)
Tam giác EAK và tam giác ECB có: \(\frac{{EA}}{{EC}} = \frac{{EK}}{{EB}}\), góc BEC chung. Do đó, $\Delta EAK\backsim \Delta ECB\left( c.g.c \right)$ nên \(\widehat {EKA} = \widehat {EBC}\)
Bài 6 trang 75 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các định lý liên quan đến tam giác đồng dạng. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và biết cách áp dụng chúng vào các bài toán cụ thể.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 6 trang 75, học sinh cần phải chứng minh một số đẳng thức liên quan đến tỉ lệ các cạnh của tam giác đồng dạng. Việc hiểu rõ yêu cầu của đề bài sẽ giúp học sinh lựa chọn phương pháp giải phù hợp và tránh những sai sót không đáng có.
Để giải bài 6 trang 75, học sinh cần nắm vững các kiến thức sau:
Bài 6: Cho tam giác ABC có AB = 6cm, AC = 9cm, BC = 12cm. Gọi D là điểm trên cạnh AC sao cho AD = 4cm. Gọi E là điểm trên cạnh BC sao cho BE = 3cm. Chứng minh rằng DE song song với AB.
Chứng minh:
(Lưu ý: Lời giải trên dựa trên đề bài gốc. Nếu đề bài có sự thay đổi về số liệu, lời giải sẽ cần được điều chỉnh tương ứng.)
Để củng cố kiến thức về tam giác đồng dạng, học sinh có thể làm thêm các bài tập tương tự sau:
Khi giải các bài tập về tam giác đồng dạng, học sinh nên:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải bài 6 trang 75 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 và các bài tập tương tự. Chúc các em học tốt!