Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải bài 6 trang 60 sách bài tập Toán 8 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Cho tam giác ABC cân tại A, có hai đường cao BE và CD \(\left( {D \in AB,E \in AC} \right)\). Chứng minh tứ giác BDEC là hình thang cân.
Đề bài
Cho tam giác ABC cân tại A, có hai đường cao BE và CD \(\left( {D \in AB,E \in AC} \right)\). Chứng minh tứ giác BDEC là hình thang cân.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về dấu hiệu nhận biết hình thang cân để chứng minh: Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Lời giải chi tiết
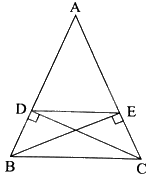
Vì tam giác ABC cân tại A nên \(AB = AC\) và \(\widehat {ABC} = \widehat {ACB}\)
Mà \(\widehat {ABC} + \widehat {ACB} + \widehat A = {180^0}\) nên \(\widehat {ABC} = \frac{{{{180}^0} - \widehat A}}{2}\) (1)
Tam giác AEB và tam giác ADC có:
\(\widehat {ADC} = \widehat {AEB} = {90^0},AB = AC,\widehat A\;chung\)
Do đó, \(\Delta AEB = \Delta ADC\left( {ch - gn} \right)\). Suy ra \(AD = AE\)
Do đó, tam giác AED cân tại E. Suy ra: \(\widehat {ADE} = \widehat {AED}\)
Mà \(\widehat {ADE} + \widehat {AED} + \widehat A = {180^0}\) nên \(\widehat {ADE} = \frac{{{{180}^0} - \widehat A}}{2}\) (2)
Từ (1) và (2) ta có: \(\widehat {ABC} = \widehat {ADE}\)
Mà hai góc này ở vị trí đồng vị nên DE//BC
Do đó, tứ giác BDEC là hình thang
Lại có: \(\widehat {DBC} = \widehat {ECB}\) (cmt) nên tứ giác BDEC là hình thang cân
Bài 6 trang 60 sách bài tập Toán 8 - Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đại số, đặc biệt là các biểu thức chứa biến. Bài tập này thường yêu cầu học sinh vận dụng các quy tắc, công thức đã học để rút gọn biểu thức, tìm giá trị của biểu thức, hoặc chứng minh đẳng thức.
Bài 6 thường bao gồm một số câu hỏi nhỏ, mỗi câu hỏi yêu cầu thực hiện một phép biến đổi đại số cụ thể. Dưới đây là phân tích chi tiết từng dạng bài thường gặp:
Đây là dạng bài phổ biến nhất, yêu cầu học sinh sử dụng các quy tắc cộng, trừ, nhân, chia đa thức, các hằng đẳng thức đáng nhớ để đưa biểu thức về dạng đơn giản nhất. Ví dụ:
Rút gọn biểu thức: (x + 2)(x - 2) + x2
Lời giải:
Dạng bài này yêu cầu học sinh thay giá trị cụ thể của biến vào biểu thức và tính toán kết quả. Ví dụ:
Tìm giá trị của biểu thức: 3x2 - 5x + 2 khi x = -1
Lời giải:
Dạng bài này yêu cầu học sinh biến đổi một vế của đẳng thức để nó tương đương với vế còn lại. Ví dụ:
Chứng minh rằng: (x + y)2 = x2 + 2xy + y2
Lời giải:
Để củng cố kiến thức và kỹ năng giải bài tập đại số, bạn nên luyện tập thêm với các bài tập tương tự trong sách bài tập và các nguồn tài liệu khác. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán khó.
Bài 6 trang 60 sách bài tập Toán 8 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh ôn tập và củng cố kiến thức về các phép biến đổi đại số. Hy vọng với hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả trên đây, bạn sẽ giải quyết bài tập này một cách dễ dàng và đạt kết quả tốt nhất.