Bài 6 trang 63 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 63 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
Quan sát Hình 8. a) Chứng minh rằng $Delta ABCbacksim Delta DEF$.
Đề bài
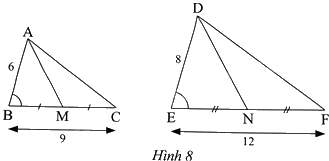
Quan sát Hình 8.
a) Chứng minh rằng $\Delta ABC\backsim \Delta DEF$.
b) Cho biết AM là đường trung tuyến của tam giác ABC, DN là đường trung tuyến của tam giác DEF và \(AM = 5,1cm\). Tính độ dài DN.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c):
+ Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.
+ Nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường trung tuyến tương ứng của hai tam giác đó cũng bằng k.
Lời giải chi tiết
a) Tam giác ABC và tam giác DEF có: \(\frac{{AB}}{{ED}} = \frac{{BC}}{{EF}}\left( { = \frac{3}{4}} \right)\), \(\widehat B = \widehat E\)
Do đó, $\Delta ABC\backsim \Delta DEF\left( c.g.c \right)$
b) Vì $\Delta ABC\backsim \Delta DEF\left( cmt \right)$ nên \(\frac{{AB}}{{ED}} = \frac{{AM}}{{DN}} = \frac{3}{4}\), suy ra \(\frac{{5,1}}{{DN}} = \frac{3}{4}\), \(DN = 6,8cm\)
Bài 6 trang 63 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải bài tập hình thang cân thường bao gồm các bước sau:
Đề bài: (Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AC và BD. Chứng minh rằng EA = EB.)
Lời giải:
Xét tam giác ACD và tam giác BCD, ta có:
Do đó, tam giác ACD = tam giác BCD (c-g-c).
Suy ra, AE = BE (các cạnh tương ứng).
Vậy, EA = EB.
Ngoài bài tập chứng minh tính chất đường chéo, học sinh có thể gặp các dạng bài tập khác liên quan đến hình thang cân, như:
Để giải các dạng bài tập này, học sinh cần nắm vững các công thức tính diện tích hình thang, đường trung bình của hình thang và các tính chất của hình thang cân.
Để củng cố kiến thức về hình thang cân, học sinh có thể tự giải các bài tập sau:
Bài 6 trang 63 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình thang cân và các tính chất của nó. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp học sinh tự tin hơn trong quá trình học tập môn Toán.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và các kiến thức bổ ích trên sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!