Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 88 sách bài tập Toán 8 Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải bài tập này ngay bây giờ!
Biểu đồ bên thống kê số đội viên tiêu biểu của các trường tiểu học trên một thị trấn tham dự một buổi giao lưu.
Đề bài
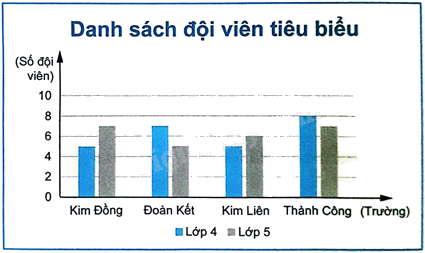
Biểu đồ bên thống kê số đội viên tiêu biểu của các trường tiểu học trên một thị trấn tham dự một buổi giao lưu. Chọn ngẫu nhiên 1 đội viên trong buổi giao lưu đó. Tính xác suất của các biến cố sau:
A: “Đội viên được chọn học lớp 5 trường Tiểu học Kim Đồng”;
B: “Đội viên được chọn học trường Tiểu học Đoàn Kết”;
C: “Đội viên được chọn học lớp 4”.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về xác suất của biến cố để tính: Khi tất cả các kết quả của một trò chơi hay một phép thử đều có khả năng xảy ra bằng nhau thì xác suất của biến cố A là tỉ số giữa số kết quả thuận lợi cho A và tổng số kết quả có thể xảy ra của phép thử, tức là:

Lưu ý: Để nhận biết các kết quả có cùng khả năng, chú ý đến các “từ khóa” liên quan đến phép thử: đồng xu, xúc xắc cân đối và đồng chất; các thẻ cùng loại, cùng kích thước; quả bóng, viên bi có cùng kích thước và khối lượng.
Lời giải chi tiết
Tổng số đội viên tham gia buổi giao lưu là: \(5 + 7 + 7 + 5 + 5 + 6 + 8 + 7 = 50\)
Do đó, có 50 kết quả có cùng khả năng xảy ra đối với phép thử chọn ngẫu nhiên 1 đội viên trong buổi giao lưu đó.
Số các kết quả thuận lợi của biến cố A là 7. Xác suất của biến cố A là: \(P\left( A \right) = \frac{7}{{50}}\)
Số các kết quả thuận lợi của biến cố B là 12. Xác suất của biến cố B là: \(P\left( B \right) = \frac{{12}}{{50}} = \frac{6}{{25}}\)
Số các kết quả thuận lợi của biến cố C là 25. Xác suất của biến cố C là: \(P\left( C \right) = \frac{{25}}{{50}} = \frac{1}{2}\)
Bài 7 trang 88 sách bài tập Toán 8 Chân trời sáng tạo tập 2 thuộc chương trình học về các tứ giác đặc biệt. Để giải bài tập này, học sinh cần nắm vững kiến thức về:
Bài tập 7 yêu cầu học sinh vận dụng kiến thức về hình thang cân và hình bình hành để giải quyết các bài toán thực tế. Thông thường, các bài tập sẽ yêu cầu:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích và giải chi tiết từng phần của bài tập. (Ở đây sẽ là nội dung giải chi tiết bài tập 7, bao gồm các bước giải, hình vẽ minh họa và giải thích rõ ràng từng bước. Nội dung này sẽ được trình bày chi tiết và đầy đủ để đảm bảo học sinh có thể hiểu và tự giải được các bài tập tương tự.)
Để củng cố kiến thức và kỹ năng giải bài tập, chúng ta sẽ cùng nhau xem xét một số ví dụ minh họa và bài tập tương tự. (Ở đây sẽ là các ví dụ minh họa và bài tập tương tự, kèm theo lời giải chi tiết để học sinh có thể luyện tập và nâng cao khả năng giải toán.)
Để giải bài tập về hình thang cân và hình bình hành một cách nhanh chóng và hiệu quả, các em cần lưu ý một số mẹo sau:
Hy vọng rằng, với lời giải chi tiết và những lưu ý quan trọng trên, các em học sinh đã có thể tự tin giải bài 7 trang 88 sách bài tập Toán 8 Chân trời sáng tạo tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Tên công thức | Nội dung |
|---|---|
| Định nghĩa hình thang cân | Hình thang có hai cạnh bên bằng nhau gọi là hình thang cân. |
| Tính chất hình thang cân | Hai góc kề một cạnh đáy bằng nhau. |
| Định nghĩa hình bình hành | Tứ giác có các cạnh đối song song là hình bình hành. |
| Tính chất hình bình hành | Các cạnh đối song song và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường. |