Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 19 trang 74 sách bài tập Toán 8 Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải cụ thể, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc (widehat {ADB},widehat {DBC}left( {E in AB,K in CD} right))
Đề bài
Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc \(\widehat {ADB},\widehat {DBC}\left( {E \in AB,K \in CD} \right)\)
a) Chứng minh DE//BK.
b) Giả sử \(DE \bot AB\). Chứng minh \(DA = DB\).
c) Trong trường hợp \(DE \bot AB\), tìm số đo của \(\widehat {ADB}\) để tứ giác DEBK là hình vuông.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai cạnh đối song song.
b) Sử dụng kiến thức về dấu hiệu nhận biết tam giác cân để chứng minh: Tam giác có đường cao đồng thời là đường phân giác thì tam giác đó là tam giác cân.
c) Sử dụng dấu hiệu nhận biết hình vuông để chứng minh: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
Lời giải chi tiết
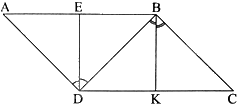
a) Vì ABCD là hình bình hành nên AD//BC. Suy ra \(\widehat {ADB} = \widehat {DBC}\) (hai góc so le trong)
Do đó: \(\frac{{\widehat {ADB}}}{2} = \frac{{\widehat {DBC}}}{2}\), suy ra \(\widehat {EDB} = \widehat {KBD}\)
Mà hai góc này ở vị trí so le trong nên DE//BK.
b) Tam giác DAB có DE vừa là đường cao đồng thời là phân giác nên tam giác DAB cân tại D. Do đó, \(DA = DB\)
c) Tứ giác DEBK có: DE//BK, EB//DK nên tứ giác DEBK là hình bình hành. Mà \(\widehat {DEB} = {90^0}\) nên DEBK là hình chữ nhật.
Để hình chữ nhật DEBK là hình vuông thì \(DE = EB\)
Mà tam giác DAB cân tại D nên DE là trung tuyến của tam giác DAB.
Suy ra: \(DE = EB = AE = \frac{{AB}}{2}\), do đó tam giác DAB vuông tại D hay \(\widehat {ADB} = {90^0}\)
Bài 19 trang 74 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc ôn tập và củng cố kiến thức về các dạng bài tập liên quan đến hình học, cụ thể là các bài toán về tứ giác. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài 19 bao gồm các bài tập khác nhau, yêu cầu học sinh vận dụng các kiến thức đã học để:
Để giải quyết các bài tập trong bài 19, học sinh cần:
Bài tập 1: Cho tứ giác ABCD có AB = CD, BC = DA. Chứng minh tứ giác ABCD là hình bình hành.
Giải:
Xét hai tam giác ABC và CDA, ta có:
Do đó, tam giác ABC bằng tam giác CDA (cạnh - cạnh - cạnh). Suy ra ∠BAC = ∠DCA và ∠BCA = ∠DAC. Vì ∠BAC = ∠DCA và ∠BCA = ∠DAC nên AB // CD và BC // DA. Vậy tứ giác ABCD là hình bình hành.
Trong bài 19, học sinh có thể gặp các dạng bài tập sau:
Để giải nhanh các bài tập về tứ giác, học sinh nên:
Học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 8:
Bài 19 trang 74 sách bài tập Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em sẽ tự tin giải quyết các bài tập trong bài và đạt kết quả tốt trong môn Toán 8.