Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 13 trang 65 sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp các bước giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các ví dụ minh họa cụ thể. Mục tiêu của chúng tôi là giúp các em học sinh học Toán 8 một cách hiệu quả nhất.
Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho \(\widehat {ADE} = \widehat {ACB}\).
Đề bài
Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho \(\widehat {ADE} = \widehat {ACB}\).
a) Chứng minh rằng $\Delta AED\backsim \Delta ABC$.
b) Tia phân giác của góc BAC cắt DE tại M và cắt BC tại N. Chứng minh rằng \(ME.NC = MD.NB\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để chứng minh: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
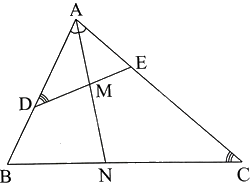
a) Xét tam giác AED và tam giác ABC có:
\(\widehat A\;chung,\widehat {ADE} = \widehat {ACB}\) (giả thiết)
Do đó, $\Delta AED\backsim \Delta ABC\left( g.g \right)$
b) Vì AM là tia phân giác của góc DAE nên \(\frac{{ME}}{{MD}} = \frac{{AE}}{{AD}}\)
Vì AN là tia phân giác của góc BAC nên \(\frac{{NB}}{{NC}} = \frac{{AB}}{{AC}}\)
Mà $\Delta AED\backsim \Delta ABC\left( cmt \right)$ nên \(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\) hay \(\frac{{AE}}{{AD}} = \frac{{AB}}{{AC}}\)
Do đó, \(\frac{{ME}}{{MD}} = \frac{{NB}}{{NC}}\). Vậy \(ME.NC = MD.NB\)
Bài 13 trang 65 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân và ứng dụng vào giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý liên quan đến hình thang cân, đồng thời rèn luyện kỹ năng chứng minh, tính toán và giải quyết vấn đề.
Bài 13 bao gồm các câu hỏi và bài tập khác nhau, được chia thành các phần nhỏ để học sinh dễ dàng tiếp cận và giải quyết. Các bài tập thường yêu cầu:
Dưới đây là lời giải chi tiết cho từng câu hỏi và bài tập trong bài 13 trang 65 sách bài tập Toán 8 - Chân trời sáng tạo tập 2:
Lời giải: (Giải thích chi tiết từng bước giải, kèm theo hình vẽ minh họa nếu cần thiết. Sử dụng các định lý, tính chất đã học để chứng minh và tính toán. Giải thích rõ ràng lý do tại sao lại sử dụng phương pháp này.)
Lời giải: (Giải thích chi tiết từng bước giải, kèm theo hình vẽ minh họa nếu cần thiết. Sử dụng các định lý, tính chất đã học để chứng minh và tính toán. Giải thích rõ ràng lý do tại sao lại sử dụng phương pháp này.)
Lời giải: (Giải thích chi tiết từng bước giải, kèm theo hình vẽ minh họa nếu cần thiết. Sử dụng các định lý, tính chất đã học để chứng minh và tính toán. Giải thích rõ ràng lý do tại sao lại sử dụng phương pháp này.)
Để giải các bài tập về hình thang cân một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Hình thang cân xuất hiện rất nhiều trong thực tế, ví dụ như:
Để củng cố kiến thức về hình thang cân, bạn có thể làm thêm các bài tập sau:
Bài 13 trang 65 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình thang cân và ứng dụng của nó trong thực tế. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 8.