Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn cách giải bài 8 trang 75 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 8 trang 75 một cách cẩn thận, kèm theo các bước giải chi tiết và dễ theo dõi.
Cho tam giác nhọn ABC, các đường cao AM, BN, CQ cắt nhau tại H. Chứng minh rằng: a) Chứng minh rằng $\Delta ANQ\backsim \Delta ABC$.
Đề bài
Cho tam giác nhọn ABC, các đường cao AM, BN, CQ cắt nhau tại H. Chứng minh rằng:
a) Chứng minh rằng $\Delta ANQ\backsim \Delta ABC$.
b) Đường thẳng QN cắt đường thẳng BC tại F. Chứng minh rằng \(FB.FC = FQ.FN\).
c) Trên đoạn HB lấy điểm I sao cho \(\widehat {AIC} = {90^0}\). Chứng minh rằng \(A{I^2} = AN.AC\).
d) Trên đoạn HC lấy điểm K sao cho \(\widehat {AKB} = {90^0}\). Chứng minh rằng \(\Delta AIK\) cân.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để chứng minh: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c) để tính chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
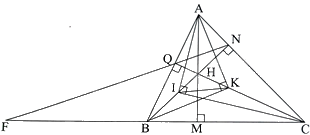
a) Chứng minh được $\Delta ANB\backsim \Delta AQC\left( g.g \right)$ suy ra \(\frac{{AN}}{{AQ}} = \frac{{AB}}{{AC}}\) hay \(\frac{{AN}}{{AB}} = \frac{{AQ}}{{AC}}\)
Tam giác ANQ và tam giác ABC có:
\(\frac{{AN}}{{AB}} = \frac{{AQ}}{{AC}}\) và góc CAB chung nên $\Delta ANQ\backsim \Delta ABC\left( c.g.c \right)$
b) Vì $\Delta ANQ\backsim \Delta ABC$ nên \(\widehat {AQN} = \widehat {NCF}\)
Mà \(\widehat {AQN} = \widehat {FQB}\) (hai góc đối đỉnh)
Do đó, \(\widehat {FQB} = \widehat {FCN}\)
Tam giác FQB và tam giác FCN có: \(\widehat {CFN}\;chung,\widehat {FQB} = \widehat {FCN}\left( {cmt} \right)\)
Do đó, $\Delta FQB\backsim \Delta FCN\left( g.g \right)$. Suy ra \(\frac{{FQ}}{{FC}} = \frac{{FB}}{{FN}}\) , suy ra \(FB.FC = FQ.FN\)
c) Chứng minh $\Delta ANI\backsim \Delta AIC\left( g.g \right)$ nên \(\frac{{AN}}{{AI}} = \frac{{AI}}{{AC}}\), do đó, \(A{I^2} = AN.AC\)
d) Chứng minh $\Delta AQK\backsim \Delta AKB\left( g.g \right)$, suy ra \(\frac{{AK}}{{AB}} = \frac{{AQ}}{{AK}}\), do đó \(A{K^2} = AB.AQ\)
mà \(AN.AC = AQ.AB\) (vì \(\frac{{AN}}{{AB}} = \frac{{AQ}}{{AC}}\)) và \(A{I^2} = AN.AC\) nên \(AI = AK\). Vậy \(\Delta AIK\) cân tại A.
Bài 8 trang 75 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các định lý liên quan.
Bài 8 yêu cầu học sinh giải quyết các bài toán liên quan đến việc chứng minh các tính chất của các hình đặc biệt. Các bài toán thường yêu cầu học sinh:
Để giải bài 8 trang 75 một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
Dưới đây là lời giải chi tiết cho từng bài tập trong bài 8 trang 75 sách bài tập Toán 8 - Chân trời sáng tạo tập 2:
Đề bài: (Ví dụ về đề bài - cần thay thế bằng đề bài thực tế)
Lời giải: (Ví dụ về lời giải - cần thay thế bằng lời giải thực tế)
Đề bài: (Ví dụ về đề bài - cần thay thế bằng đề bài thực tế)
Lời giải: (Ví dụ về lời giải - cần thay thế bằng lời giải thực tế)
Đề bài: (Ví dụ về đề bài - cần thay thế bằng đề bài thực tế)
Lời giải: (Ví dụ về lời giải - cần thay thế bằng lời giải thực tế)
Bài 8 trang 75 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các hình đặc biệt. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các bạn học sinh sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.