Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 8 trang 46 sách bài tập Toán 8 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng trình bày các bước giải một cách rõ ràng và logic nhất.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán 8, tự tin giải quyết các bài tập và đạt kết quả tốt trong học tập.
Trong các miếng bìa sau, miếng bìa nào gấp được hình chóp tam giác đều, hình chóp tứ giác đều?
Đề bài
Trong các miếng bìa sau, miếng bìa nào gấp được hình chóp tam giác đều, hình chóp tứ giác đều?
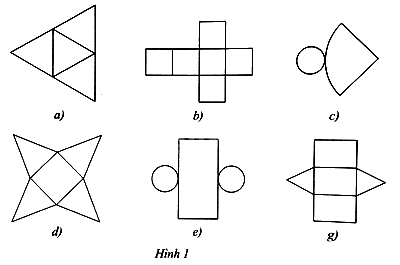
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về hình chóp tam giác đều để tìm hình đúng: Hình chóp tam giác đều là hình có đáy là hình tam giác đều, các mặt bên là các tam giác cân (tại đỉnh của hình chóp) bằng nhau.
+ Sử dụng kiến thức về hình chóp tứ giác đều để tìm hình đúng: Hình chóp tứ giác đều là hình có đáy là hình vuông, các mặt bên là các tam giác cân (tại đỉnh của hình chóp) bằng nhau.
Lời giải chi tiết
Miếng bìa ở hình 1a gấp được một hình chóp tam giác đều, miếng bìa ở hình 1d gấp được một hình chóp tứ giác đều.
Bài 8 trang 46 sách bài tập Toán 8 - Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh phải hiểu rõ định nghĩa, các tính chất đặc trưng của hình thang cân, cũng như các phương pháp chứng minh một tứ giác là hình thang cân.
Bài 8 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 8 trang 46, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi:
Cho hình thang ABCD có AB song song CD, AD = BC. Chứng minh ABCD là hình thang cân.
Lời giải:
Cho hình thang cân ABCD có AB song song CD, AB = 5cm, CD = 10cm, BC = 6cm. Tính độ dài đường cao của hình thang.
Lời giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK là đường cao của hình thang.
Ta có: HK = AB = 5cm. Suy ra, DH = KC = (CD - AB) / 2 = (10 - 5) / 2 = 2.5cm.
Xét tam giác BHC vuông tại K, ta có: BC2 = BK2 + KC2 (định lý Pitago)
Suy ra, BK2 = BC2 - KC2 = 62 - 2.52 = 36 - 6.25 = 29.75
Vậy, BK = √29.75 ≈ 5.45cm. Đường cao của hình thang là 5.45cm.
Để giải tốt các bài tập về hình thang cân, các em học sinh cần:
Ngoài sách giáo khoa và sách bài tập, các em học sinh có thể tham khảo thêm các tài liệu sau:
Bài 8 trang 46 sách bài tập Toán 8 - Chân trời sáng tạo là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hình thang cân. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong học tập.