Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 75 sách bài tập Toán 8 - Chân trời sáng tạo tập 2. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 8.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để các em hiểu rõ bản chất của bài toán.
Một người dùng thước êke để đo chiều cao từ chân đến mắt người đó là 1,6m và đứng cách trục chính tòa nhà 4,8m (Hình 5). Hỏi tòa nhà cao khoảng bao nhiêu?
Đề bài
Một người dùng thước êke để đo chiều cao từ chân đến mắt người đó là 1,6m và đứng cách trục chính tòa nhà 4,8m (Hình 5). Hỏi tòa nhà cao khoảng bao nhiêu?
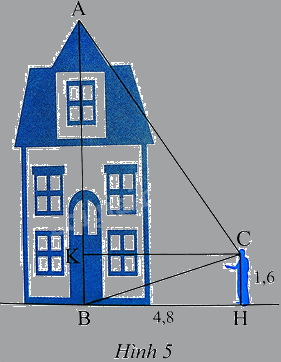
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để tính: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
Ta có: \(\widehat A = \widehat {BCK}\) (cùng phụ với góc KCA).
Lại có: KC//BH (cùng vuông góc với KB) nên \(\widehat {BCK} = \widehat {CBH}\) (hai góc so le trong)
Do đó, \(\widehat A = \widehat {HBC}\)
Tam giác AKC và tam giác BHC có: \(\widehat {AKC} = \widehat {BHC} = {90^0},\widehat A = \widehat {HBC}\) (cmt)
Do đó, $\Delta AKC\backsim \Delta BHC\left( g.g \right)$, suy ra \(\frac{{AK}}{{BH}} = \frac{{CK}}{{HC}}\), hay \(\frac{{AK}}{{4,8}} = \frac{{4,8}}{{1,6}}\)
Do đó, \(AK = \frac{{4,8.4,8}}{{1,6}} = 14,4\left( m \right)\). Vậy độ cao của tòa nhà là: \(14,4 + 1,6 = 16\left( m \right)\)
Bài 5 trang 75 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân và ứng dụng vào giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các định lý, tính chất đã học và biết cách áp dụng chúng một cách linh hoạt.
Bài 5 trang 75 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 5 trang 75 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 một cách hiệu quả, các em cần thực hiện theo các bước sau:
Bài toán: Cho hình thang cân ABCD (AB // CD), AB = 6cm, CD = 10cm, AD = BC = 5cm. Tính chiều cao của hình thang.
Giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK là chiều cao của hình thang.
Ta có: DH = KC = (CD - AB) / 2 = (10 - 6) / 2 = 2cm.
Áp dụng định lý Pitago vào tam giác ADH vuông tại H, ta có:
AH2 = AD2 - DH2 = 52 - 22 = 21.
Vậy, AH = √21 cm.
Chiều cao của hình thang ABCD là √21 cm.
Khi giải các bài toán về hình thang cân, các em cần lưu ý những điều sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập sau:
Bài 5 trang 75 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về hình thang cân và ứng dụng của nó. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin giải quyết bài tập một cách hiệu quả. Chúc các em học tốt!