Bài 3 trang 45 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các dạng bài tập liên quan đến hình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 45 sách bài tập Toán 8 - Chân trời sáng tạo tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC, hai đường trung tuyến BM và CN cắt nhau tại G \(\left( {M \in AC,N \in AB} \right)\). Gọi D, E lần lượt là trung điểm của GB, GC. Chứng minh:
Đề bài
Cho tam giác ABC, hai đường trung tuyến BM và CN cắt nhau tại G \(\left( {M \in AC,N \in AB} \right)\). Gọi D, E lần lượt là trung điểm của GB, GC. Chứng minh:
a) MN//DE
b) ND//ME
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+ Sử dụng kiến thức về tính chất của đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
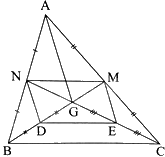
a) Vì BM và CN là các đường trung tuyến của tam giác ABC nên \(AM = MC,AN = NB\)
Tam giác ABC có: \(AM = MC,AN = NB\) nên MN là đường trung bình của tam giác ABC.
Do đó, \(MN//BC,MN = \frac{1}{2}BC\)
Tam giác GBC có: D, E lần lượt là trung điểm của GB, GC nên DE là đường trung bình của tam giác GBC.
Do đó, DE//BC, \(DE = \frac{1}{2}BC\)
Ta có: MN//BC, DE//BC nên MN//DE
b) Tứ giác MNDE có: MN//DE, \(MN = DE\left( { = \frac{{BC}}{2}} \right)\)
Do đó, tứ giác MNDE là hình bình hành. Do đó, ND//ME
Bài 3 trang 45 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học đã được học để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Phương pháp giải bài toán thường bao gồm các bước sau:
Đề bài: (Giả sử đề bài là: Cho hình vẽ, biết góc A = 60 độ. Tính góc B.)
Lời giải:
Vì góc A và góc B là hai góc kề bù nên:
A + B = 180 độ
Thay A = 60 độ vào, ta có:
60 độ + B = 180 độ
B = 180 độ - 60 độ
B = 120 độ
Vậy, góc B = 120 độ.
Ngoài bài 3 trang 45, sách bài tập Toán 8 - Chân trời sáng tạo tập 2 còn có nhiều bài tập tương tự về góc và đường thẳng. Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức và phương pháp giải đã được trình bày ở trên. Một số dạng bài tập thường gặp bao gồm:
Để rèn luyện kỹ năng giải toán, học sinh nên làm thêm nhiều bài tập khác nhau và tham khảo các tài liệu học tập bổ sung.
Khi giải bài tập về góc và đường thẳng, học sinh cần lưu ý một số điểm sau:
Bài 3 trang 45 sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về góc và đường thẳng. Bằng cách nắm vững các kiến thức và phương pháp giải đã được trình bày, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.