Bài 15 trang 51 sách bài tập Toán 8 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh phải vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 15 trang 51, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC vuông tại A có \(AB = 6cm,AC = 8cm\). Tia phân giác của \(\widehat {ABC}\) cắt AC tại D.
Đề bài
Cho tam giác ABC vuông tại A có \(AB = 6cm,AC = 8cm\). Tia phân giác của \(\widehat {ABC}\) cắt AC tại D.
a) Tính độ dài DA, DC.
b) Tia phân giác của \(\widehat {ACB}\) cắt BD ở I. Gọi M là trung điểm của BC. Chứng minh \(\widehat {BIM} = {90^0}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất của đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
Lời giải chi tiết
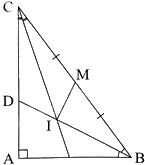
a) Áp dụng định lí Pythagore vào tam giác ABC vuông tại A có: \(BC = \sqrt {A{B^2} + A{C^2}} = 10\left( {cm} \right)\)
Vì BD là tia phân giác của góc ABC trong tam giác ABC nên theo tính chất đường phân giác của tam giác ta có: \(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\)
Do đó, \(\frac{{DA}}{3} = \frac{{DC}}{5} = \frac{{AC}}{8} = 1\). Suy ra: \(DA = 3cm,DC = 5cm\)
b) Áp dụng định lí Pythagore vào tam giác ABD vuông tại A có: \(BD = \sqrt {A{B^2} + A{D^2}} = 3\sqrt 5 \left( {cm} \right)\)
Vì CI là đường phân giác của góc DCB trong tam giác BCD nên theo tính chất đường phân giác của tam giác ta có: \(\frac{{ID}}{{IB}} = \frac{{DC}}{{BC}} = \frac{5}{{10}} = \frac{1}{2}\), suy ra \(\frac{{ID}}{1} = \frac{{IB}}{2} = \frac{{BD}}{3} = \sqrt 5 \)
Suy ra: \(ID = \sqrt 5 cm,IB = 2\sqrt 5 cm\)
Chứng minh \(\Delta IDC = \Delta IMC\left( {c - g - c} \right)\) nên \(IM = ID = \sqrt 5 cm\)
Vì \(I{M^2} + I{B^2} = 25 = M{B^2}\) nên tam giác IMB vuông tại I (định lí Pythagore đảo). Do đó, \(\widehat {BIM} = {90^0}\)
Bài 15 trang 51 sách bài tập Toán 8 Chân trời sáng tạo tập 2 thuộc chương trình học Toán 8, tập trung vào việc củng cố kiến thức về các phép biến đổi đại số, đặc biệt là các phép toán với đa thức. Bài tập này thường bao gồm các dạng toán như:
Để giải quyết bài 15 trang 51 một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Giả sử câu a yêu cầu phân tích đa thức x^2 - 4 thành nhân tử. Ta có thể sử dụng hằng đẳng thức a^2 - b^2 = (a - b)(a + b) để phân tích như sau:
x^2 - 4 = x^2 - 2^2 = (x - 2)(x + 2)
Giả sử câu b yêu cầu rút gọn biểu thức (x + 1)(x - 1) + 2x. Ta thực hiện các bước sau:
(x + 1)(x - 1) = x^2 - 1x^2 - 1 + 2xx^2 + 2x - 1Việc giải bài 15 trang 51 không chỉ giúp học sinh củng cố kiến thức về đại số mà còn là nền tảng quan trọng cho các bài học tiếp theo. Kỹ năng phân tích đa thức, rút gọn biểu thức đại số và giải phương trình bậc nhất một ẩn là những kỹ năng cần thiết cho việc học Toán ở các lớp trên.
Học sinh có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về bài học:
Bài 15 trang 51 sách bài tập Toán 8 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đại số. Hy vọng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học Toán 8.