Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn cách giải bài 2 trang 71 sách bài tập Toán 8 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho tam giác DEF vuông tại D \(\left( {DE > DF} \right)\), DM là đường trung tuyến \(\left( {M \in EF} \right)\).
Đề bài
Cho tam giác DEF vuông tại D \(\left( {DE > DF} \right)\), DM là đường trung tuyến \(\left( {M \in EF} \right)\). Gọi MN là đường vuông góc kẻ từ M đến DE \(\left( {N \in DE} \right)\), MK là đường vuông góc kẻ từ M đến DF \(\left( {K \in DF} \right)\), H là điểm đối xứng với M qua N.
a) Tứ giác DKMN là hình gì? Vì sao?
b) Gọi O là trung điểm của DM. Chứng minh ba điểm H, O, F thẳng hàng.
c) Tam giác DEF cần thêm điều kiện gì để tứ giác KDMN là hình vuông?
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về dấu hiệu của hình chữ nhật để chứng minh: Tứ giác có ba góc vuông là hình chữ nhật.
b) + Sử dụng kiến thức về dấu hiệu của hình bình hành để chứng minh: Tứ hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+ Sử dụng kiến thức về tính chất của hình bình hành để chứng minh: Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.
+ Sử dụng kiến thức về tính chất của hình chữ nhật để chứng minh: Hình chữ nhật có hai đường chéo bằng nhau cắt nhau tại trung điểm mỗi đường.
c) Sử dụng kiến thức về dấu hiệu nhận biết hình vuông để chứng minh: Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
Lời giải chi tiết
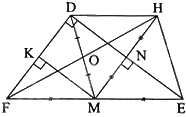
a) Vì tam giác DEF vuông tại D nên \(\widehat {EDF} = {90^0}\)
Vì MN là đường vuông góc kẻ từ M đến DE nên \(\widehat {MNE} = \widehat {MND} = {90^0}\)
Vì MK là đường vuông góc kẻ từ M đến DF nên \(\widehat {MKF} = \widehat {MKD} = {90^0}\)
Tứ giác DKMN có: \(\widehat {EDF} = \widehat {MND} = \widehat {MKD} = {90^0}\) nên tứ giác DKMN là hình chữ nhật.
b) Tam giác DEF vuông tại D nên DM là đường trung tuyến ứng với cạnh huyền nên \(MD = \frac{1}{2}EF = ME\)
Do đó, tam giác MDE cân tại M.
Lại có: \(MN \bot DE\) nên MN là đường cao đồng thời là đường trung tuyến của tam giác MDE.
Do đó, \(ND = NE = \frac{1}{2}DE\)
Tứ giác DHEM có: \(ND = NE = \frac{1}{2}DE\), \(NH = NM = \frac{{HM}}{2}\) (vì H là điểm đối xứng với M qua N) nên tứ giác DHEM mà là hình bình hành. Do đó, \(DH = ME\), DH//ME
Mà M là trung điểm của EF nên \(ME = MF\), do đó \(DH = MF\)
Tứ giác DHMF có: \(DH = MF\), DH//MF
Do đó, tứ giác DHMF là hình bình hành.
Mà O là trung điểm của DM nên O cũng là trung điểm của HF. Do đó, ba điểm H, O, F thẳng hàng.
c) Hình chữ nhật DKMN là hình vuông khi DM là đường phân giác của góc KDN hay DM là đường phân giác của góc EDF.
Khi đó, DM là đường trung tuyến đồng thời là đường phân giác xuất phát từ đỉnh D của tam giác DEF.
Suy ra, tam giác DEF vuông cân tại D.
Bài 2 trang 71 sách bài tập Toán 8 - Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý liên quan đến hình thang cân để có thể giải quyết một cách chính xác.
Bài 2 yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 2 trang 71, chúng tôi xin trình bày lời giải chi tiết như sau:
Giả sử hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ, AD = BC là các cạnh bên. Để tính độ dài các cạnh, ta cần sử dụng các thông tin đã cho trong đề bài và áp dụng các công thức liên quan đến hình thang cân.
Ví dụ, nếu đề bài cho biết AB = 10cm, CD = 6cm, AD = 5cm, ta có thể tính độ dài BC bằng cách sử dụng tính chất AD = BC, do đó BC = 5cm.
Trong hình thang cân, hai góc kề một đáy bằng nhau và hai góc kề một cạnh bên thì bù nhau. Do đó, để tính các góc của hình thang cân, ta cần xác định các góc đã cho và sử dụng các tính chất trên để tính các góc còn lại.
Ví dụ, nếu đề bài cho biết góc A = 80 độ, ta có thể tính góc B bằng cách sử dụng tính chất góc A = góc B, do đó góc B = 80 độ. Sau đó, ta có thể tính góc C và góc D bằng cách sử dụng tính chất góc A + góc D = 180 độ và góc B + góc C = 180 độ.
Để chứng minh các tính chất liên quan đến hình thang cân, ta cần sử dụng các định nghĩa, định lý đã học và áp dụng các phương pháp chứng minh hình học như chứng minh hai tam giác bằng nhau, chứng minh hai đường thẳng song song, v.v.
Ví dụ, để chứng minh hai đường chéo của hình thang cân bằng nhau, ta có thể chứng minh hai tam giác tạo bởi hai đường chéo và các cạnh đáy bằng nhau theo trường hợp cạnh - góc - cạnh.
Để giải bài tập hình thang cân một cách hiệu quả, các em học sinh có thể tham khảo một số mẹo sau:
Kiến thức về hình thang cân có ứng dụng rộng rãi trong thực tế, chẳng hạn như trong kiến trúc, xây dựng, thiết kế đồ họa, v.v. Ví dụ, hình thang cân thường được sử dụng trong thiết kế mái nhà, cầu, cửa sổ, v.v.
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài 2 trang 71 sách bài tập Toán 8 - Chân trời sáng tạo và tự tin hơn trong quá trình học tập. Chúc các em học tốt!