Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 72 sách bài tập Toán 8 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án, cách giải và giải thích chi tiết từng bước để giúp các em hiểu rõ kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Cho hình bình hành MNPQ có O là giao điểm của hai đường chéo. Biết \(MN = 6,OM = 3,ON = 4\). Độ dài của MP, NQ, PQ lần lượt là
Đề bài
Cho hình bình hành MNPQ có O là giao điểm của hai đường chéo. Biết \(MN = 6,OM = 3,ON = 4\). Độ dài của MP, NQ, PQ lần lượt là
A. 6; 8; 6
B. 8; 6; 6
C. 6; 6; 8
D. 8; 8; 6
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất hình bình hành: Trong hình bình hành:
+ Hai cạnh đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết
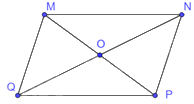
Vì MNPQ là hình bình hành nên \(PQ = MN = 6,NQ = 2ON = 8,MP = 2OM = 6\)
Chọn A
Bài 5 trang 72 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương ôn tập, nhằm giúp học sinh củng cố kiến thức đã học trong chương. Bài tập tập trung vào việc vận dụng các kiến thức về hình học, đặc biệt là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Việc giải bài tập này đòi hỏi học sinh phải nắm vững các định nghĩa, định lý và công thức liên quan.
Bài 5 bao gồm các dạng bài tập sau:
Đề bài: Cho hình bình hành ABCD. Gọi E là trung điểm của AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng: a) Tam giác ADE = Tam giác BCE. b) F là trung điểm của AC.
Lời giải:
Đề bài: Cho hình chữ nhật ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng: a) OA = OB = OC = OD. b) ∠OAB = ∠OBA.
Lời giải:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh đã hiểu rõ cách giải bài 5 trang 72 sách bài tập Toán 8 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!