Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 12 trang 74 sách bài tập Toán 8 Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải cụ thể, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho tứ giác EKIT có \(EK = ET,IK = IT,\widehat {KET} = {90^0},\widehat {EKI} = {105^0}\).
Đề bài
Cho tứ giác EKIT có \(EK = ET,IK = IT,\widehat {KET} = {90^0},\widehat {EKI} = {105^0}\). Gọi S là giao điểm của hai đường chéo. Tính số đo các góc \(\widehat {KIS},\widehat {SKI}\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về đường chéo của tứ giác để tìm số đo góc còn lại: Trong tứ giác, đường chéo là đoạn thẳng nối hai đỉnh đối nhau
Lời giải chi tiết
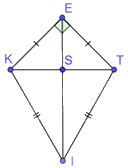
Vì \(EK = ET\) nên E thuộc đường trung trực của KT.
Vì \(IK = IT\) nên I thuộc đường trung trực của KT.
Do đó, EI là đường trung trực của KT. Suy ra: \(EI \bot KT\) tại S.
Tam giác EKT có: \(EK = ET\), \(\widehat {KET} = {90^0}\) nên tam giác EKT vuông cân tại E. Do đó, ES là đường trung trực đồng thời là đường phân giác. Do đó, \(\widehat {KES} = \frac{1}{2}\widehat {KET} = {45^0}\)
Tam giác KEI có: \(\widehat {KIE} = {180^0} - \widehat {EKI} - \widehat {KES} = {30^0}\)
Tam giác KIS vuông tại S có: \(\widehat {SKI} = {90^0} - \widehat {KIS} = {90^0} - {30^0} = {60^0}\)
Bài 12 trang 74 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý liên quan đến hình thang cân để giải quyết các bài toán thực tế.
Bài 12 trang 74 sách bài tập Toán 8 Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 12 trang 74, chúng ta sẽ đi vào phân tích từng phần của bài tập. (Giả sử bài tập cụ thể là: Cho hình thang cân ABCD (AB // CD), có AB = 5cm, CD = 10cm, AD = 6cm. Tính chiều cao của hình thang.)
Vẽ hình thang cân ABCD với AB // CD, AB = 5cm, CD = 10cm, AD = 6cm. Kẻ đường cao AH và BK (H, K thuộc CD). Khi đó, AH = BK và DH = KC.
Ta có: DH + KC = CD - AB = 10cm - 5cm = 5cm. Vì DH = KC nên DH = KC = 5cm / 2 = 2.5cm.
Trong tam giác vuông ADH, ta có: AH2 + DH2 = AD2. Suy ra: AH2 = AD2 - DH2 = 62 - 2.52 = 36 - 6.25 = 29.75.
Vậy, AH = √29.75 ≈ 5.45cm.
Chiều cao của hình thang cân ABCD là khoảng 5.45cm.
Để giải tốt các bài tập về hình thang cân, học sinh cần lưu ý những điều sau:
Học sinh có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về hình thang cân:
Bài 12 trang 74 sách bài tập Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình thang cân. Hy vọng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.