Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 8. Bài viết này sẽ hướng dẫn bạn giải bài 2 trang 65 sách bài tập toán 8 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy logic và vận dụng kiến thức đã học. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, chi tiết, kèm theo các bước giải cụ thể để bạn có thể dễ dàng theo dõi và nắm bắt.
Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD. a) Chứng minh rằng tứ giác AHCK là hình bình hành.
Đề bài
Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh \(AN = CM.\)
c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về dấu hiệu của hình bình hành để chứng minh: Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.
b) Sử dụng kiến thức về dấu hiệu của hình bình hành để chứng minh: Tứ giác có hai cặp cạnh đối song song là hình bình hành.
c) Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết
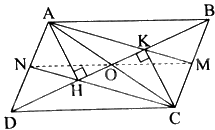
a) Vì ABCD là hình bình hành (gt) nên \(AD = BC\), AD//CB. Do đó, \(\widehat {HDA} = \widehat {KBC}\) (hai góc so le trong)
Vì \(HA \bot BD\) nên \(\widehat {AHD} = \widehat {AHB} = {90^0}\)
Vì \(CK \bot BD\) nên \(\widehat {BKC} = \widehat {DKC} = {90^0}\)
Tam giác ADH và tam giác CKB có:
\(\widehat {AHD} = \widehat {CKB} = {90^0}\), \(\widehat {HDA} = \widehat {KBC}\) (cmt), \(AD = BC\)
Do đó, \(\Delta ADH = \Delta CBK\left( {ch - gn} \right)\). Suy ra \(AH = KC\).
Tứ giác AHCK có: AH//CK (cùng vuông góc với BD), \(AH = KC\) nên tứ giác AHCK là hình bình hành.
b) Vì tứ giác AHCK là hình bình hành nên AK//HC hay AM//NC
Tứ giác ANCM có: AM//NC (cmt), AN//CM (cmt)
Do đó, tứ giác ANCM là hình bình hành.
Suy ra: \(AN = CM.\)
c) Vì tứ giác AHCK là hình bình hành nên hai đường chéo AC, HK cắt nhau tại trung điểm O của HK nên O là trung điểm của AC.
Vì tứ giác ANCM là hình bình hành nên hai đường chéo AC, NM cắt nhau tại trung điểm O của AC nên O là trung điểm của MN. Do đó, M, O, N thẳng hàng.
Bài 2 trang 65 sách bài tập toán 8 - Chân trời sáng tạo thuộc chương trình học toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các định nghĩa, định lý và tính chất liên quan đến các hình này.
Trước khi bắt tay vào giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của đề. Trong bài 2 trang 65, đề bài thường yêu cầu chứng minh một đẳng thức hình học, tính toán diện tích hoặc chu vi của một hình, hoặc giải một bài toán thực tế liên quan đến các hình đã học.
Để minh họa, chúng ta sẽ cùng giải một bài tập cụ thể thuộc bài 2 trang 65. Giả sử đề bài yêu cầu: “Cho hình chữ nhật ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng OA = OB = OC = OD.”
Như vậy, chúng ta đã chứng minh được OA = OB = OC = OD.
Bài 2 trang 65 thường xuất hiện các dạng bài tập sau:
Để giải các bài tập này, bạn cần:
Để nắm vững kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách bài tập và các nguồn tài liệu khác. Bạn cũng có thể tham khảo các bài giảng trực tuyến hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán từ lớp 6 đến lớp 12. Chúng tôi hy vọng rằng bài viết này đã giúp bạn giải bài 2 trang 65 sách bài tập toán 8 - Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tốt!