Bài 5 trang 63 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 63 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
Quan sát Hình 7. Chứng minh rằng \(\widehat {OBA} = \widehat {OAC}\).
Đề bài
Quan sát Hình 7. Chứng minh rằng \(\widehat {OBA} = \widehat {OAC}\).
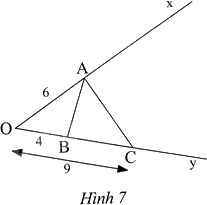
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c) để chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
Tam giác OAB và tam giác OCA có: \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OA}}\left( { = \frac{2}{3}} \right)\), góc O chung.
Do đó, $\Delta OAB\backsim \Delta OCA\left( c.g.c \right)$ nên \(\widehat {OBA} = \widehat {OAC}\)
Bài 5 trang 63 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải bài tập hình thang cân thường bao gồm:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hình thang cân ABCD có AB // CD, AD = BC. Gọi E là giao điểm của AC và BD. Chứng minh rằng AE = BE.)
Lời giải:
Xét tam giác ADC và tam giác BCD, ta có:
Do đó, tam giác ADC và tam giác BCD bằng nhau theo trường hợp cạnh - góc - cạnh (c-g-c).
Suy ra AE = BE (các cạnh tương ứng).
Vậy, AE = BE.
Ngoài bài 5 trang 63, Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 còn có nhiều bài tập tương tự về hình thang cân. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức và phương pháp giải đã trình bày ở trên. Ngoài ra, cần chú ý đến việc vẽ hình minh họa và phân tích đề bài một cách cẩn thận.
Để củng cố kiến thức về hình thang cân, học sinh có thể tự giải thêm các bài tập sau:
Bài 5 trang 63 Sách bài tập Toán 8 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình thang cân và các tính chất của nó. Hy vọng với lời giải chi tiết và phương pháp giải đã trình bày, các em học sinh sẽ tự tin hơn khi làm bài tập về hình thang cân.