Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 sách Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 10 trang 11, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.
Từ một tấm tôn hình chữ nhật có chiều dài bằng a (cm), chiều rộng bằng b (cm), người ta cắt bỏ bốn hình vuông cạnh bằng x (cm) ở bốn góc,
Đề bài
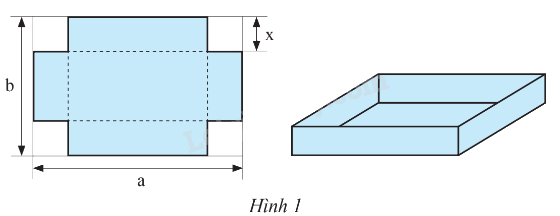
Từ một tấm tôn hình chữ nhật có chiều dài bằng a (cm), chiều rộng bằng b (cm), người ta cắt bỏ bốn hình vuông cạnh bằng x (cm) ở bốn góc, rồi gấp và hàn thành thùng không có nắp (Hình 1). Viết biểu thức biểu thị:
a) Thể tích nước tối đa mà thùng có thể chứa được.
b) Tổng diện tích của năm mặt của chiếc thùng.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức nhân đơn thức với đa thức: Để nhân đơn thức với đa thức ta nhân đơn thức đó với từng hạng tử của đa thức, rồi cộng các kết quả với nhau.
+ Sử dụng kiến thức cộng trừ hai đa thức để tính:
+ Sử dụng kiến thức nhân hai đa thức để tính: Để nhân hai đa thức, ta lấy từng hạng tử của đa thức này nhân với đa thức kia, rồi cộng các kết quả với nhau.
Lời giải chi tiết
Thùng trên có chiều dài là: \(a - 2x\left( {cm} \right)\), chiều rộng là \(b - 2x\left( {cm} \right)\), chiều cao là x (cm)
a) Thể tích của thùng là:
\(V = \left( {a - 2x} \right)\left( {b - 2x} \right)x = \left[ {a\left( {b - 2x} \right) - 2x\left( {b - 2x} \right)} \right]x\)
\( = \left( {ab - 2ax - 2bx + 4{x^2}} \right)x = abx - 2a{x^2} - 2b{x^2} + 4{x^3}\)
Vậy thể tích nước tối đa mà thùng có thể chứa được là \(abx - 2a{x^2} - 2b{x^2} + 4{x^3}\left( {c{m^3}} \right)\)
b) Tổng diện tích năm mặt của chiếc thùng là:
\(S = \left( {a - 2x} \right)\left( {b - 2x} \right) + 2x\left( {a - 2x} \right) + 2x\left( {b - 2x} \right)\)
\( = a\left( {b - 2x} \right) - 2x\left( {b - 2x} \right) + 2ax - 4{x^2} + 2bx - 4{x^2}\)
\( = ab - 2ax - 2bx + 4{x^2} + 2ax - 4{x^2} + 2bx - 4{x^2}\)
\( = ab + \left( {2ax - 2ax} \right) + \left( {2bx - 2bx} \right) + \left( {4{x^2} - 4{x^2} - 4{x^2}} \right) = ab - 4{x^2}\)
Vậy tổng diện tích của năm mặt của chiếc thùng là \(ab - 4{x^2}\left( {c{m^2}} \right)\)
Bài 10 trang 11 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về đa thức, đơn thức và các phép toán trên chúng. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm cơ bản, cũng như kỹ năng thực hiện các phép tính một cách chính xác.
Bài 10 trang 11 thường bao gồm các dạng bài tập sau:
Để giải bài 10 trang 11 sách bài tập Toán 8 Chân trời sáng tạo một cách hiệu quả, bạn có thể tham khảo các bước sau:
Bài tập: Rút gọn biểu thức sau: 3x2 + 2x - 5x2 + 7x - 3
Giải:
3x2 + 2x - 5x2 + 7x - 3 = (3x2 - 5x2) + (2x + 7x) - 3
= -2x2 + 9x - 3
Để giải các bài tập về đa thức, đơn thức một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và kỹ năng giải bài tập về đa thức, đơn thức, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 8 Chân trời sáng tạo, hoặc tìm kiếm trên các trang web học toán online.
Bài 10 trang 11 sách bài tập Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đa thức, đơn thức và các phép toán trên chúng. Hy vọng với hướng dẫn chi tiết và các mẹo giải nhanh trên đây, bạn sẽ tự tin hơn trong việc giải bài tập này và đạt kết quả tốt trong môn Toán.