Chào mừng các em học sinh đến với lời giải chi tiết bài 9 trang 7 sách bài tập Toán 8 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải bài 9 trang 7 ngay bây giờ!
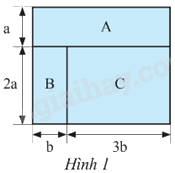
Cho ba hình chữ nhật A, B, C với các kích thước như Hình 1. Tính diện tích của mỗi hình chữ nhật này và tổng diện tích của chúng.
Đề bài
Cho ba hình chữ nhật A, B, C với các kích thước như Hình 1. Tính diện tích của mỗi hình chữ nhật này và tổng diện tích của chúng.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về đa thức thu gọn để thu gọn các đa thức: Đa thức thu gọn là đa thức không chứa hai hạng tử nào đồng dạng.
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.
+ Sử dụng kiến thức về đơn thức thu gọn để thu gọn các đơn thức: Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến chỉ xuất hiện một lần dưới dạng nâng lên lũy thừa với số mũ nguyên dương.
Diện tích hình chữ nhật bằng tích hai kích thước của nó.
Lời giải chi tiết
Hình chữ nhật A có hai kích thước là a và \(b + 3b = 4b\) nên diện tích của hình chữ nhật A là: \(4ab\)
Hình chữ nhật B có hai kích thước là 2a và b nên diện tích của hình chữ nhật B là: \(2ab\)
Hình chữ nhật C có hai kích thước là 2a và 3b nên diện tích của hình chữ nhật C là: \(2a.3b = 6ab\)
Tổng diện tích của ba hình chữ nhật A, B, C là: \(4ab + 2ab + 6ab = 12ab\)
Bài 9 trang 7 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học về các phép biến đổi đơn giản với đa thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về thu gọn đa thức, tìm bậc của đa thức, và thực hiện các phép cộng, trừ đa thức để giải quyết các bài toán cụ thể.
Bài 9 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để thu gọn đa thức này, ta thực hiện cộng các hạng tử đồng dạng:
2x2 - 5x2 + 3x + 7x - 2 = (2 - 5)x2 + (3 + 7)x - 2 = -3x2 + 10x - 2
Vậy đa thức thu gọn là -3x2 + 10x - 2.
Bậc của đa thức là bậc của hạng tử có bậc cao nhất. Trong đa thức -3x2 + 10x - 2, hạng tử có bậc cao nhất là -3x2, có bậc là 2.
Vậy bậc của đa thức là 2.
Để tính giá trị của đa thức tại x = 1, ta thay x = 1 vào đa thức:
-3(1)2 + 10(1) - 2 = -3 + 10 - 2 = 5
Vậy giá trị của đa thức tại x = 1 là 5.
Để cộng hai đa thức, ta cộng các hạng tử đồng dạng:
(x2 + 2x2) + (-2x + x) + (1 - 3) = 3x2 - x - 2
Vậy kết quả của phép cộng là 3x2 - x - 2.
Kiến thức về các phép biến đổi đơn giản với đa thức có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học, đặc biệt là trong việc giải phương trình, bất phương trình, và các bài toán liên quan đến hàm số.
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 8 Chân trời sáng tạo hoặc trên các trang web học toán online.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã hiểu rõ cách giải bài 9 trang 7 sách bài tập Toán 8 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!