Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải bài 5 trang 57 sách bài tập Toán 8 chương trình Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Cho tứ giác ABCD có \(\widehat C - \widehat D = {10^0}\). Các tia phân giác của góc A và góc B cắt nhau tại I. Biết \(\widehat {AIB} = {65^0}\). Tính góc C và góc D.
Đề bài
Cho tứ giác ABCD có \(\widehat C - \widehat D = {10^0}\). Các tia phân giác của góc A và góc B cắt nhau tại I. Biết \(\widehat {AIB} = {65^0}\). Tính góc C và góc D.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tổng các góc của một tứ giác để tính góc: Tổng số đo các góc của một tứ giác bằng 360 độ.
Lời giải chi tiết
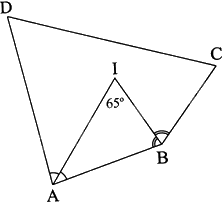
Tam giác AIB có: \(\widehat {AIB} + \widehat {IAB} + \widehat {IBA} = {180^0}\)
Suy ra: \(\widehat {IAB} + \widehat {IBA} = {180^0} - \widehat {AIB} = {115^0}\)
Vì AI là tia phân giác của góc DAB nên \(\widehat {DAB} = 2\widehat {IAB}\)
Vì BI là tia phân giác của góc ABC nên \(\widehat {ABC} = 2\widehat {ABI}\)
Do đó: \(\widehat {ABC} + \widehat {DAB} = 2\left( {\widehat {IAB} + \widehat {IBA}} \right) = {230^0}\)
Tứ giác ABCD có: \(\widehat C + \widehat D = {360^0} - \left( {\widehat {ABC} + \widehat {DAB}} \right) = {130^0}\)
Mà \(\widehat C - \widehat D = {10^0}\) nên \(\widehat C = {10^0} + \widehat D\)
Do đó: \(2\widehat D + {10^0} = {130^0}\), do đó \(\widehat D = {60^0}\), suy ra \(\widehat C = {60^0} + {10^0} = {70^0}\)
Bài 5 trang 57 sách bài tập Toán 8 Chân trời sáng tạo thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Bài tập này thường yêu cầu học sinh vận dụng các tính chất của hình thang cân để giải quyết các vấn đề liên quan đến độ dài cạnh, góc, đường trung bình và đường cao. Việc nắm vững kiến thức lý thuyết và kỹ năng giải bài tập là rất quan trọng để đạt kết quả tốt trong môn Toán.
Bài 5 trang 57 thường bao gồm các dạng bài tập sau:
Để giải bài 5 trang 57 sách bài tập Toán 8 Chân trời sáng tạo một cách hiệu quả, bạn có thể làm theo các bước sau:
Bài toán: Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi M là trung điểm của AD, N là trung điểm của BC. Chứng minh rằng MN là đường trung bình của hình thang.
Lời giải:
Gọi I là giao điểm của AC và BD. Vì ABCD là hình thang cân nên AC = BD. Do đó, tam giác AIC = tam giác BID (c-g-c). Suy ra AI = BI và CI = DI.
Xét tam giác ACD, M là trung điểm của AD và I là trung điểm của AC. Do đó, MI là đường trung bình của tam giác ACD. Suy ra MI // CD và MI = 1/2 CD.
Xét tam giác BCD, N là trung điểm của BC và I là trung điểm của BD. Do đó, NI là đường trung bình của tam giác BCD. Suy ra NI // CD và NI = 1/2 CD.
Từ MI // CD và NI // CD suy ra MI // NI. Vì MI = 1/2 CD và NI = 1/2 CD nên MI = NI.
Do đó, MN là đường trung bình của hình thang ABCD.
Để học tốt môn Toán 8, bạn có thể tham khảo các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 5 trang 57 sách bài tập Toán 8 Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tốt và đạt kết quả cao trong môn Toán!