Bài 1 (10.7) trang 94 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các phép toán trên số hữu tỉ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1 (10.7) trang 94 Vở thực hành Toán 7 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Kể tên các đỉnh, cạnh và đường chéo của hình lập phương MNPQ. EFGH ở Hình 10.6.
Đề bài
Kể tên các đỉnh, cạnh và đường chéo của hình lập phương MNPQ. EFGH ở Hình 10.6.
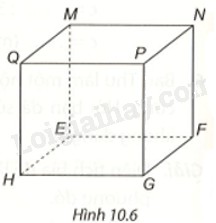
Phương pháp giải - Xem chi tiết
+ Hình hộp chữ nhật như hình vẽ dưới:
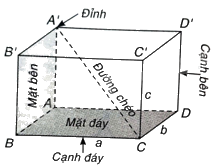
+ Hình lập phương là hình hộp chữ nhật có 6 mặt là các hình vuông.
Lời giải chi tiết
Hình lập phương trong Hình 10.6 có các đỉnh, cạnh và đường chéo, là:
- Các đỉnh: M, N, P, Q, E, F, G, H.
- Các cạnh đáy: EF, PQ, MN, NP, QM, FG, GH, HE.
- Các cạnh bên: ME, PG, NF, QH.
- Các đường chéo: MG, NH, PE, QF.
Bài 1 (10.7) trang 94 Vở thực hành Toán 7 tập 2 thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng thực hiện các phép tính với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về số hữu tỉ, các phép cộng, trừ, nhân, chia số hữu tỉ, và quy tắc dấu ngoặc.
Bài 1 (10.7) trang 94 Vở thực hành Toán 7 tập 2 thường bao gồm các dạng bài tập sau:
Để giải bài 1 (10.7) trang 94 Vở thực hành Toán 7 tập 2, học sinh có thể áp dụng các phương pháp sau:
Bài tập: Tính giá trị của biểu thức sau: (1/2 + 1/3) * 4/5
Giải:
Bước 1: Tính giá trị trong ngoặc:
1/2 + 1/3 = 3/6 + 2/6 = 5/6
Bước 2: Thực hiện phép nhân:
5/6 * 4/5 = 20/30 = 2/3
Vậy, giá trị của biểu thức (1/2 + 1/3) * 4/5 là 2/3.
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, học sinh có thể tự luyện tập với các bài tập sau:
Bài 1 (10.7) trang 94 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng thực hiện các phép tính với số hữu tỉ. Bằng cách nắm vững kiến thức cơ bản, áp dụng các phương pháp giải đúng đắn, và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập về số hữu tỉ một cách hiệu quả.