Chào mừng các em học sinh đến với lời giải chi tiết bài 2 (9.21) trang 77, 78 Vở thực hành Toán 7 tập 2. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Chứng minh rằng: a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau. b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Đề bài
Chứng minh rằng:
a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.
b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Phương pháp giải - Xem chi tiết
a) + Giả sử tam giác ABC cân tại A và có BN, CP là hai đường trung tuyến. Ta cần chứng minh \(BN = CP\).
+ Chứng minh \(\Delta BCP = \Delta CBN\left( {c.g.c} \right)\), suy ra \(CP = BN\).
b) + Giả sử BN, CP là hai đường trung tuyến của tam giác ABC, \(BN = CP\). Ta sẽ chứng minh \(AB = AC\).
+ Gọi G là trọng tâm của tam giác ABC.
+ Chứng minh \(\Delta PGB = \Delta NGC\left( {c.g.c} \right)\), suy ra \(BP = NC\). Do đó, \(AB = 2BP = 2CN = AC\).
Lời giải chi tiết
(H.9.22)
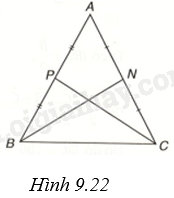
a) Tam giác ABC cân tại A và có BN, CP là hai đường trung tuyến. Ta cần chứng minh \(BN = CP\).
Tam giác ABC cân tại A nên \(AB = AC\).
Do N, P lần lượt là trung điểm của AC, AB nên \(BP = \frac{1}{2}AB,CN = \frac{1}{2}AC\), do đó \(BP = CN\).
Xét hai tam giác BCP và CBN, ta có:
\(BP = CN\), \(\widehat {BPC} = \widehat {NCB}\), BC chung nên \(\Delta BCP = \Delta CBN\left( {c.g.c} \right)\).
Suy ra \(CP = BN\).
b) BN, CP là hai đường trung tuyến của tam giác ABC, \(BN = CP\). Ta sẽ chứng minh \(AB = AC\).
Gọi G là trọng tâm của tam giác ABC.
Xét hai tam giác PGB và NGC, ta có:
\(PG = NG,BG = GC,\widehat {PGB} = \widehat {NGC}\) (đối đỉnh)
Vậy \(\Delta PGB = \Delta NGC\left( {c.g.c} \right)\), suy ra \(BP = NC\).
Do đó, \(AB = 2BP = 2CN = AC\)
Vậy tam giác ABC cân tại A.
Bài 2 (9.21) trang 77, 78 Vở thực hành Toán 7 tập 2 thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về tỉ số, tỉ lệ thức để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm cơ bản và biết cách áp dụng chúng vào các tình huống cụ thể.
Bài tập 2 (9.21) thường bao gồm các dạng bài sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập.
Đề bài: Cho tỉ lệ thức \frac{a}{b} = \frac{c}{d}\. Chứng minh rằng \frac{a+b}{a-b} = \frac{c+d}{c-d}\.
Lời giải:
Đề bài: Chia số 120 thành ba phần tỉ lệ với 2, 3, 5.
Lời giải:
Gọi ba phần cần chia là x, y, z. Theo đề bài, ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\frac{x}{2} = \frac{y}{3} = \frac{z}{5} = \frac{x+y+z}{2+3+5} = \frac{120}{10} = 12\
Từ đó, ta có:
Vậy, ba phần cần chia lần lượt là 24, 36, 60.
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập trên, các em sẽ tự tin hơn khi giải bài 2 (9.21) trang 77, 78 Vở thực hành Toán 7 tập 2. Chúc các em học tập tốt!