Chào mừng các em học sinh đến với lời giải chi tiết bài 7 (7.17) trang 36 Vở thực hành Toán 7 tập 2. Bài học này thuộc chương trình Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trên một mảnh đất hình chữ nhật có chiều dài 65m, người ta định làm một bể bơi có chiều rộng là x mét, chiều dài gấp 3 lần chiều rộng. Sơ đồ và kích thước cụ thể (tính bằng mét) được cho trong hình bên. Tìm đa thức (biến x): a) Biểu thị diện tích của bể bơi. b) Biểu thị diện tích mảnh đất. c) Biểu thị diện tích phần đất xung quanh bể bơi.
Đề bài
Trên một mảnh đất hình chữ nhật có chiều dài 65m, người ta định làm một bể bơi có chiều rộng là x mét, chiều dài gấp 3 lần chiều rộng. Sơ đồ và kích thước cụ thể (tính bằng mét) được cho trong hình bên.
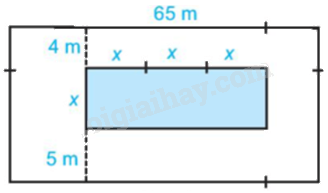
Tìm đa thức (biến x):
a) Biểu thị diện tích của bể bơi.
b) Biểu thị diện tích mảnh đất.
c) Biểu thị diện tích phần đất xung quanh bể bơi.
Phương pháp giải - Xem chi tiết
+ Diện tích hình chữ nhật = chiều dài. chiều rộng.
+ Diện tích phần đất xung quanh= Diện tích mảnh đất – diện tích bể bơi.
Lời giải chi tiết
a) Bể bơi có dạng hình chữ nhật với chiều rộng là x mét, chiều dài là 3x mét.
Biểu thức biểu thị diện tích của nó là \({S_1} = x.3x = 3{x^2}\left( {{m^2}} \right)\).
b) Miếng đất cũng có dạng hình chữ nhật với chiều rộng là \(x + 9\left( m \right)\), chiều dài là 65m.
Biểu thức biểu thị diện tích của nó là \({S_2} = \left( {x + 9} \right).65 = 65x + 585\left( {{m^2}} \right)\).
c) Diện tích phần đất quanh bể bơi là:
\({S_2} - {S_1} = \left( {65x + 585} \right) - 3{x^2} = - 3{x^2} + 65x + 585\)
Vậy đa thức biểu thị diện tích phần đất xung quanh bể bơi là: \(S = - 3{x^2} + 65x + 585\).
Bài 7 (7.17) trang 36 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán liên quan đến các phép toán với số hữu tỉ. Bài tập này yêu cầu học sinh phải nắm vững các quy tắc cộng, trừ, nhân, chia số hữu tỉ, cũng như các tính chất của phép toán để có thể giải quyết bài toán một cách chính xác và hiệu quả.
Bài tập 7 (7.17) thường bao gồm các dạng bài sau:
Để giải bài tập 7 (7.17) trang 36 Vở thực hành Toán 7 tập 2 một cách hiệu quả, học sinh cần:
Dưới đây là lời giải chi tiết cho bài tập 7 (7.17) trang 36 Vở thực hành Toán 7 tập 2. (Lưu ý: Nội dung lời giải cụ thể sẽ phụ thuộc vào đề bài cụ thể của bài tập 7.17. Ví dụ minh họa:)
Tính: (-1/2) + (3/4) - (-5/6)
Giải:
Để tính biểu thức này, ta cần tìm mẫu số chung nhỏ nhất của 2, 4 và 6. Mẫu số chung nhỏ nhất là 12.
Ta có:
(-1/2) = (-6/12)
(3/4) = (9/12)
(-5/6) = (-10/12)
Vậy, (-1/2) + (3/4) - (-5/6) = (-6/12) + (9/12) - (-10/12) = (-6 + 9 + 10)/12 = 13/12
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể tham khảo các bài tập tương tự sau:
Bài tập 7 (7.17) trang 36 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán với số hữu tỉ. Bằng cách nắm vững các quy tắc, tính chất và phương pháp giải, các em có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Phép toán | Quy tắc |
|---|---|
| Cộng, trừ số hữu tỉ | Quy đồng mẫu số, cộng/trừ tử số, giữ nguyên mẫu số |
| Nhân số hữu tỉ | Nhân tử số với tử số, mẫu số với mẫu số |
| Chia số hữu tỉ | Nhân số bị chia với nghịch đảo của số chia |