Bài 2 (9.8) trang 69, 70 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho tam giác cân ABC, (AB = AC). Lấy điểm M tùy ý nằm giữa B và C (H.9.7). a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất. b) Chứng minh rằng với mọi điểm M thì (AM < AB).
Đề bài
Cho tam giác cân ABC, \(AB = AC\). Lấy điểm M tùy ý nằm giữa B và C (H.9.7).
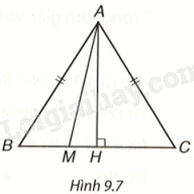
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
b) Chứng minh rằng với mọi điểm M thì \(AM < AB\).
Phương pháp giải - Xem chi tiết
+ Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
+ Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Lời giải chi tiết
a) Kẻ đường cao AH của tam giác ABC, ta có AH là đường vuông góc hạ từ điểm A xuống BC. Gọi M là điểm tùy ý nằm giữa B và C. Nếu M khác H thì AM là đường xiên kẻ từ A đến BC. Do đó theo định lí, \(AH < AM\). Vậy AM nhỏ nhất bằng AH khi M trùng H.
b) M là một điểm nằm giữa B và C. Ta cần chứng minh \(AM < AB\). Muốn vậy, ta xét các trường hợp sau:
Trường hợp 1: Nếu \(\widehat {AMB} = {90^o}\), thì AM là đường vuông góc, còn AB là đường xiên kẻ từ A xuống BC theo định lí về đường vuông góc và đường xiên, ta có \(AM < AB\).
Trường hợp 2: Nếu \(\widehat {AMB}\) là góc tù thì trong tam giác AMB, góc AMB lớn nhất nên \(AM < AB\).
Trường hợp 3: Nếu \(\widehat {AMB}\) là góc nhọn thì góc AMC kề bù với nó là góc tù. Trong tam giác AMC, góc AMC là góc lớn nhất. Do đó, \(AM < AC = AB\).
Bài 2 (9.8) trang 69, 70 Vở thực hành Toán 7 tập 2 yêu cầu học sinh thực hiện các phép tính với số hữu tỉ, thường liên quan đến việc cộng, trừ, nhân, chia các phân số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về phép tính với số hữu tỉ, bao gồm:
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Xác định các số hữu tỉ cần thực hiện phép tính và loại phép tính cần sử dụng. Việc phân tích đề bài giúp học sinh tránh được những sai sót không đáng có.
Dưới đây là lời giải chi tiết cho bài 2 (9.8) trang 69, 70 Vở thực hành Toán 7 tập 2. (Lưu ý: Vì đề bài cụ thể không được cung cấp, phần này sẽ trình bày một ví dụ minh họa về cách giải một bài tập tương tự.)
Mẫu số chung nhỏ nhất của 2, 3 và 6 là 6. Ta quy đồng các phân số như sau:
Thay các phân số đã quy đồng vào biểu thức ban đầu, ta có:
(1/2) + (2/3) - (1/6) = (3/6) + (4/6) - (1/6) = (3 + 4 - 1)/6 = 6/6 = 1
Ngoài bài tập trực tiếp yêu cầu thực hiện các phép tính, bài 2 (9.8) trang 69, 70 Vở thực hành Toán 7 tập 2 có thể xuất hiện dưới các dạng bài tập khác nhau, như:
Để giải các dạng bài tập này, học sinh cần:
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, học sinh nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa, sách bài tập và các nguồn tài liệu học tập khác. Việc luyện tập thường xuyên sẽ giúp học sinh tự tin hơn khi đối mặt với các bài toán khó.
Bài 2 (9.8) trang 69, 70 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về số hữu tỉ. Bằng cách nắm vững các quy tắc, phân tích đề bài và luyện tập thường xuyên, học sinh có thể giải bài tập này một cách dễ dàng và hiệu quả.