Bài 3 (4.25) trang 73 Vở thực hành Toán 7 là một bài tập quan trọng trong chương trình học Toán lớp 7. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và phương pháp giải khoa học cho bài tập này, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài 3 (4.25). Cho tam giác ABC và M là trung điểm BC. a) Giả sử AM vuông góc với BC. Chứng minh rẳng \(\Delta ABC\)cân tại A. b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rẳng \(\Delta ABC\)cân tại A.
Đề bài
Bài 3 (4.25). Cho tam giác ABC và M là trung điểm BC.
a) Giả sử AM vuông góc với BC. Chứng minh rẳng \(\Delta ABC\)cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rẳng \(\Delta ABC\)cân tại A.
Phương pháp giải - Xem chi tiết
Tam giác cân là tam giác có hai cạnh bằng nhau.
Lời giải chi tiết
a)
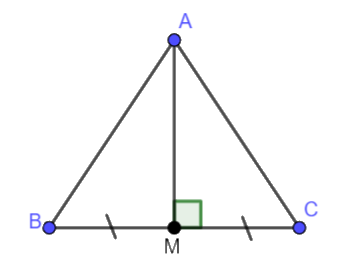
GT | \(\Delta ABC\), \(M \in BC,MB = MC,AM \bot BC\) |
KL | \(\Delta ABC\)cân tại A |
Ta thấy hai tam giác ABM và ACM vuông tại đỉnh M và có:
MB = MC
AM là cạnh chung
Vậy \(\Delta ABM = \Delta ACM\)(hai cạnh góc vuông). Do đó AB = AC hay \(\Delta ABC\)cân tại A.
b)
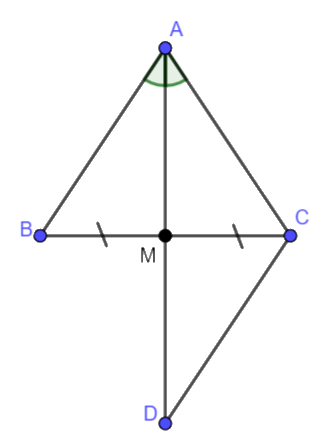
GT | \(\Delta ABC\), \(M \in BC,MB = MC,\widehat {MAB} = \widehat {MAC}\) |
KL | \(\Delta ABC\)cân tại A |
Kéo dài AM một đoạn MD sao cho MD = MA.
Hai tam giác MAB và MDC có
MB = MC (theo giả thiết)
\(\widehat {AMB} = \widehat {CMD}\)(hai góc đối đỉnh)
MA = MD (theo cách dựng)
Vậy \(\Delta MAB = \Delta MDC\)(c – g – c). Do đó AB = DC (1)
Mặt khác \(\Delta ACD\)có \(\widehat {CAD} = \widehat {BAM} = \widehat {CDM} = \widehat {CDA}\)
Vậy \(\Delta ACD\)cân tại C và do đó AC = CD (2)
Từ (1) và (2) suy ra AB = AC hay \(\Delta ABC\)cân tại A.
Bài 3 (4.25) trang 73 Vở thực hành Toán 7 thuộc chương trình học Toán lớp 7, tập trung vào việc vận dụng các kiến thức về số hữu tỉ và các phép toán trên số hữu tỉ vào giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc tính toán liên quan.
Đề bài yêu cầu thực hiện các phép tính sau:
Để giải các bài tập này, chúng ta cần tuân thủ thứ tự thực hiện các phép toán: trong ngoặc trước, nhân chia trước, cộng trừ sau.
Vậy, (1/2 + 1/3) * (2/3 - 1/2) = 5/36
Vậy, (5/4 - 2/3) : (1/2 + 3/4) = 7/15
Vậy, 2/5 * (3/8 + (-1/4)) = 1/20
Vậy, (1/2 - 3/5) * (1/3 - 1/4) = -1/120
Để củng cố kiến thức về số hữu tỉ và các phép toán trên số hữu tỉ, bạn có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và vở bài tập Toán 7.
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 3 (4.25) trang 73 Vở thực hành Toán 7. Chúc bạn học tốt!