Giải bài 2 (3.28) trang 51 vở thực hành Toán 7

Giải bài 2 (3.28) trang 51 Vở thực hành Toán 7: Hướng dẫn chi tiết và phương pháp giải

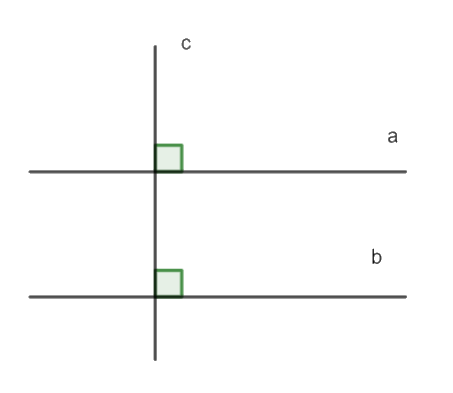
Bài 2 (3.28) trang 51 Vở thực hành Toán 7 thuộc chương trình Toán lớp 7, tập trung vào việc rèn luyện kỹ năng thực hiện các phép tính với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về cộng, trừ, nhân, chia số hữu tỉ, cũng như các tính chất giao hoán, kết hợp, phân phối của các phép toán này.

Nội dung bài tập

Bài 2 (3.28) trang 51 Vở thực hành Toán 7 thường bao gồm các dạng bài tập sau:

• Tính giá trị của các biểu thức chứa số hữu tỉ.
• Tìm x trong các phương trình đơn giản với số hữu tỉ.
• Giải các bài toán thực tế liên quan đến số hữu tỉ.

Phương pháp giải

Để giải bài 2 (3.28) trang 51 Vở thực hành Toán 7, học sinh có thể áp dụng các phương pháp sau:

1. Quy đồng mẫu số: Khi thực hiện các phép cộng, trừ số hữu tỉ, ta cần quy đồng mẫu số để đưa các phân số về cùng mẫu số, sau đó cộng hoặc trừ các tử số và giữ nguyên mẫu số.
2. Rút gọn phân số: Trước khi thực hiện các phép tính, ta nên rút gọn các phân số về dạng tối giản để đơn giản hóa phép tính.
3. Sử dụng tính chất giao hoán, kết hợp, phân phối: Áp dụng các tính chất này để biến đổi biểu thức và tìm ra kết quả một cách dễ dàng.
4. Chuyển đổi các dạng biểu thức: Chuyển đổi các biểu thức từ dạng phân số sang dạng số thập phân hoặc ngược lại để thuận tiện cho việc tính toán.

Ví dụ minh họa

Ví dụ 1: Tính giá trị của biểu thức sau: A = 1/2 + 2/3 - 5/6

Giải:

Ta quy đồng mẫu số của các phân số: 1/2 = 3/6 và 2/3 = 4/6

Vậy, A = 3/6 + 4/6 - 5/6 = (3 + 4 - 5)/6 = 2/6 = 1/3

Ví dụ 2: Tìm x trong phương trình: x + 1/4 = 3/2

Giải:

x = 3/2 - 1/4

Ta quy đồng mẫu số: 3/2 = 6/4

Vậy, x = 6/4 - 1/4 = 5/4

Luyện tập thêm

Để nắm vững kiến thức và kỹ năng giải bài 2 (3.28) trang 51 Vở thực hành Toán 7, học sinh nên luyện tập thêm các bài tập tương tự. Dưới đây là một số bài tập gợi ý:

• Tính giá trị của các biểu thức sau: B = 2/5 - 1/3 + 4/15, C = (1/2 + 1/3) * 6/5
• Tìm x trong các phương trình sau: x - 2/7 = 1/3, 3/4 * x = 9/8

Lời khuyên

Khi giải bài tập về số hữu tỉ, học sinh cần chú ý:

• Đọc kỹ đề bài và xác định đúng yêu cầu của bài tập.
• Sử dụng các quy tắc và tính chất của các phép toán số học một cách chính xác.
• Kiểm tra lại kết quả sau khi giải xong bài tập.

Giaitoan.edu.vn hy vọng với hướng dẫn chi tiết và phương pháp giải trên, các em học sinh sẽ tự tin giải bài 2 (3.28) trang 51 Vở thực hành Toán 7 và đạt kết quả tốt trong môn Toán.