Chào mừng các em học sinh đến với lời giải chi tiết bài 1 (9.14) trang 74 Vở thực hành Toán 7 tập 2. Bài học này thuộc chương trình Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các biểu thức đại số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
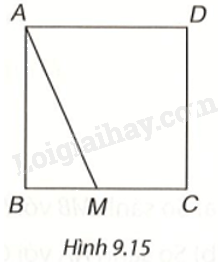
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.15).
Đề bài
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.15).
Phương pháp giải - Xem chi tiết
Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.
Lời giải chi tiết
Khi M trùng B (hoặc D) thì AM = a \(\left( {AB = a} \right)\) với a là độ dài cạnh hình vuông. Khi M khác B, M thuộc cạnh BC thì tam giác ABM vuông tại B nên AM là cạnh huyền, do đó \(a = AB < AM\). Tương tự, khi M khác D, M thuộc cạnh CD, ta có $a=AD<AM$.
Bài 1 (9.14) trang 74 Vở thực hành Toán 7 tập 2 yêu cầu chúng ta thực hiện các phép tính với biểu thức đại số. Cụ thể, đề bài thường bao gồm các biểu thức chứa biến, số và các phép toán cộng, trừ, nhân, chia. Mục tiêu của bài tập là giúp học sinh rèn luyện kỹ năng biến đổi biểu thức, áp dụng các quy tắc về thứ tự thực hiện các phép toán và đơn giản hóa biểu thức.
Để giải quyết bài tập này một cách hiệu quả, chúng ta cần nắm vững các phương pháp sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 1 (9.14) trang 74 Vở thực hành Toán 7 tập 2. (Lưu ý: Nội dung lời giải chi tiết sẽ được trình bày cụ thể cho từng biểu thức trong bài tập. Ví dụ:)
Lời giải:
Thay x = 2 và y = -1 vào biểu thức, ta có:
3x + 2y = 3 * 2 + 2 * (-1) = 6 - 2 = 4
Vậy, giá trị của biểu thức 3x + 2y khi x = 2 và y = -1 là 4.
Lời giải:
5a - 3b + 2a - b = (5a + 2a) + (-3b - b) = 7a - 4b
Vậy, biểu thức 5a - 3b + 2a - b được rút gọn thành 7a - 4b.
Để củng cố kiến thức và kỹ năng giải bài tập về biểu thức đại số, các em có thể tham khảo các bài tập tương tự sau:
Kiến thức về biểu thức đại số là nền tảng quan trọng cho việc học Toán ở các lớp trên. Việc nắm vững các quy tắc, tính chất và phương pháp giải bài tập về biểu thức đại số sẽ giúp các em tự tin giải quyết các bài toán phức tạp hơn trong tương lai.
Hy vọng rằng, với lời giải chi tiết và các phương pháp giải bài tập được trình bày ở trên, các em học sinh đã có thể tự tin giải bài 1 (9.14) trang 74 Vở thực hành Toán 7 tập 2 và các bài tập tương tự. Chúc các em học tập tốt!