Bài 5 trang 83 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ, đặc biệt là các phép cộng, trừ, nhân, chia.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 83 VTH Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho (Delta ABC) vuông tại A. Tia phân giác của (widehat {ABC}) cắt AC tại E. Từ E kẻ (EH bot BC) tại H và EH cắt AB tại K. a) Chứng minh (AE = EH). b) So sánh độ dài hai cạnh AE và EC. c) Chứng minh BE là đường trung trực của AH. d) Chứng minh (Delta KBC) là tam giác cân.
Đề bài
Cho \(\Delta ABC\) vuông tại A. Tia phân giác của \(\widehat {ABC}\) cắt AC tại E. Từ E kẻ \(EH \bot BC\) tại H và EH cắt AB tại K.
a) Chứng minh \(AE = EH\).
b) So sánh độ dài hai cạnh AE và EC.
c) Chứng minh BE là đường trung trực của AH.
d) Chứng minh \(\Delta KBC\) là tam giác cân.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta ABE = \Delta HBE\) (cạnh huyền – góc nhọn), suy ra \(AE = EH\).
b) Chứng minh \(EH < EC\), kết hợp \(AE = EH\) suy ra \(AE < EC\).
c) Chứng minh tam giác ABH cân tại B, suy ra có BE là đường phân giác cũng là đường trung trực của AH.
d) Chứng minh E là trực tâm của tam giác KBC, suy ra BE là đường cao của tam giác KBC. Kết hợp với BE là đường phân giác của tam giác KBC, suy ra tam giác KBC cân tại B.
Lời giải chi tiết
(H.9.37)
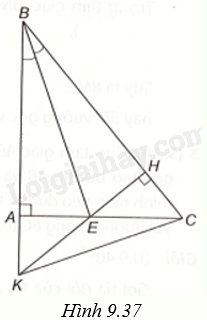
a) Xét \(\Delta ABE\) và \(\Delta HBE\) có: BE chung, \(\widehat {ABE} = \widehat {EBH}\), \(\widehat {BAE} = \widehat {BHE} = {90^o}\)
Do đó, \(\Delta ABE = \Delta HBE\) (cạnh huyền – góc nhọn)
Suy ra \(AE = EH\) (hai cạnh tương ứng).
b) Trong tam giác vuông EHC, ta có EC là cạnh huyền nên \(EH < EC\), mà \(AE = EH\)(cmt) nên \(AE < EC\).
c) Từ \(\Delta ABE = \Delta HBE\), suy ra \(AB = HB\) (hai cạnh tương ứng), suy ra tam giác ABH cân tại B có BE là đường phân giác nên BE cũng là đường trung trực của AH.
d) Tam giác KBC có hai đường cao CA và KH cắt nhau tại E nên E là trực tâm của tam giác KBC, do đó BE là đường cao của tam giác KBC.
Mặt khác có BE là đường phân giác của tam giác KBC nên BE vừa là đường cao vừa là đường phân giác của tam giác KBC, suy ra tam giác KBC cân tại B.
Bài 5 trang 83 Vở thực hành Toán 7 tập 2 thuộc chương trình học về số hữu tỉ. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán cụ thể. Việc nắm vững các quy tắc và kỹ năng này là nền tảng quan trọng cho việc học toán ở các lớp trên.
Bài 5 trang 83 Vở thực hành Toán 7 tập 2 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 5 trang 83 Vở thực hành Toán 7 tập 2, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Giả sử bài tập có 3 câu a, b, c)
Ví dụ: Tính: (-1/2) + (3/4) - (-5/6)
Lời giải:
Ví dụ: Tìm x biết: x + (2/3) = (5/6)
Lời giải:
Ví dụ: Một cửa hàng có 200kg gạo. Ngày đầu bán được 1/4 số gạo, ngày thứ hai bán được 2/5 số gạo còn lại. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Lời giải:
Để giải các bài tập về số hữu tỉ một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, bạn nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp bạn tự tin hơn trong quá trình học tập.
Bài 5 trang 83 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về số hữu tỉ. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.