Bài 10 trang 110, 111 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng giải bài toán về tỉ lệ thức và ứng dụng vào các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 110, 111 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho (BD = BA) và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt BA tại M. Chứng minh rằng: a) (Delta ABH = Delta DBH). b) Tam giác AED cân. c) (EM > ED). d) Tam giác BCM là tam giác đều và (CE = 2EA), biết (widehat {ABC} = {60^o}).
Đề bài
Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho \(BD = BA\) và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt BA tại M. Chứng minh rằng:
a) \(\Delta ABH = \Delta DBH\).
b) Tam giác AED cân.
c) \(EM > ED\).
d) Tam giác BCM là tam giác đều và \(CE = 2EA\), biết \(\widehat {ABC} = {60^o}\).
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta ABH = \Delta DBH\) (c.c.c).
b) Chứng minh\(\Delta BAE = \Delta BDE\) (c.g.c) suy ra \(EA = ED\), suy ra tam giác AED cân.
c) + Chứng minh \(\Delta EAM = \Delta EDC\) (g.c.g). Suy ra \(EM = EC\)
+ \(\Delta EDC\) vuông tại D nên \(EC > ED\). Do đó, \(EM > ED\).
d) + Chỉ ra \(AM = DC\), mà \(BA = BD\) nên \(BM = BC\), suy ra \(\Delta BMC\) cân tại B.
+ Lại có \(\widehat {ABC} = {60^o}\) nên \(\Delta BMC\) là tam giác đều.
+ Chứng minh CA, MD là đường cao cũng là đường trung tuyến của \(\Delta BMC\), suy ra E là trọng tâm của \(\Delta BMC\) nên \(CE = 2EA\).
Lời giải chi tiết
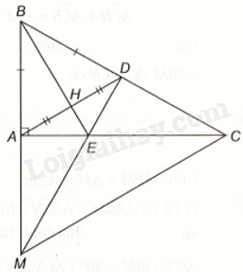
a) \(\Delta ABH\) và \(\Delta DBH\) có:
\(BA = BD\) (theo giả thiết).
BH là cạnh chung
\(AH = DH\) (H là trung điểm của AD)
Nên \(\Delta ABH = \Delta DBH\) (c.c.c).
b) Ta có: \(\Delta ABH = \Delta DBH\) (chứng minh trên), suy ra \(\widehat {ABE} = \widehat {DBE}\) (hai góc tương ứng)
\(\Delta BAE\) và \(\Delta BDE\) có:
\(BA = BD\) (giả thiết).
\(\widehat {ABE} = \widehat {DBE}\) (chứng minh trên)
BE là cạnh chung
Nên \(\Delta BAE = \Delta BDE\) (c.g.c) suy ra \(EA = ED\) (hai cạnh tương ứng).
Nên \(\Delta ADE\) cân tại E (dấu hiệu nhận biết tam giác cân).
c) \(\Delta BAE = \Delta BDE\) (chứng minh trên) nên \(\widehat {BDE} = \widehat {BAE} = {90^o}\).
\(\Delta EAM\) và \(\Delta EDC\) có:
\(\widehat {EAM} = \widehat {EDC} = {90^o}\),
\(EA = ED\) (chứng minh trên),
\(\widehat {AEM} = \widehat {DEC}\) (hai góc đối đỉnh).
Nên \(\Delta EAM = \Delta EDC\) (g.c.g). Suy ra \(EM = EC\).
\(\Delta EDC\) vuông tại D nên \(EC > ED\) (quan hệ giữa cạnh và góc trong tam giác).
Mà \(EC = EM\) (chứng minh trên) nên \(EM > ED\).
d) Ta có \(\Delta EAM = \Delta EDC\) (chứng minh trên) suy ra \(AM = DC\) (hai cạnh tương ứng).
Mà \(BA = BD\) (giả thiết) nên \(BM = BC\).
\(\Delta BMC\) có: \(BM = BC\) (chứng minh trên)
Nên \(\Delta BMC\) cân tại B (dấu hiệu nhận biết tam giác cân).
Mà \(\widehat {ABC} = {60^o}\). Nên \(\Delta BMC\) là tam giác đều.
Mặt khác \(CA \bot BM\) nên CA là đường cao cũng là đường trung tuyến của \(\Delta BMC\), \(MD \bot BC\) nên MD là đường cao cũng là đường trung tuyến của \(\Delta BMC\).
Từ đó suy ra E là trọng tâm của \(\Delta BMC\) nên \(CE = 2EA\).
Bài 10 trang 110, 111 Vở thực hành Toán 7 tập 2 thuộc chương trình học Toán 7, tập trung vào việc vận dụng kiến thức về tỉ lệ thức để giải quyết các bài toán thực tế. Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, Giaitoan.edu.vn xin trình bày chi tiết lời giải và hướng dẫn từng bước.
Bài 10 yêu cầu học sinh giải các bài toán liên quan đến việc tìm hai số khi biết tỉ số và tổng (hoặc hiệu) của chúng. Đây là một dạng toán thường gặp trong chương trình Toán 7 và có ứng dụng rộng rãi trong cuộc sống.
Để giải bài toán này, chúng ta có thể sử dụng phương pháp sau:
Bài 10a: Tìm hai số a và b biết a:b = 3:5 và a + b = 24.
Giải:
Bài 10b: Tìm hai số x và y biết x:y = 2:3 và x - y = 10.
Giải:
Bài 10c: Tìm hai số m và n biết m:n = 1:2 và m + n = 30.
Giải:
Khi giải các bài toán về tỉ lệ thức, cần chú ý:
Bài tập về tỉ lệ thức có ứng dụng rộng rãi trong nhiều lĩnh vực của cuộc sống, như:
Việc nắm vững kiến thức về tỉ lệ thức sẽ giúp học sinh giải quyết các bài toán thực tế một cách dễ dàng và hiệu quả.
Bài 10 trang 110, 111 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán về tỉ lệ thức. Hy vọng với lời giải chi tiết và hướng dẫn từng bước của Giaitoan.edu.vn, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập này và tự tin giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục kiến thức Toán học. Chúc các em học tập tốt!