Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 62 Vở thực hành Toán 7. Bài học này thuộc chương trình Toán 7 tập 1, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài 7. Cho các điểm A, B, C, D như hình dưới đây. Biết \(\Delta ADC = \Delta BCD\), hãy chứng minh \(\Delta ADB = \Delta BCA\).
Đề bài
Bài 7. Cho các điểm A, B, C, D như hình dưới đây. Biết \(\Delta ADC = \Delta BCD\), hãy chứng minh \(\Delta ADB = \Delta BCA\).
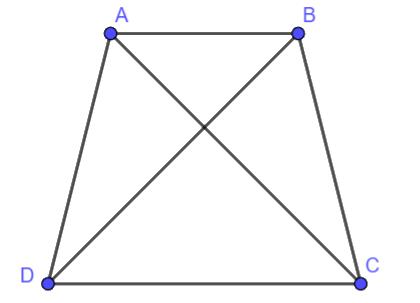
Phương pháp giải - Xem chi tiết
Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh .
Lời giải chi tiết
Vì \(\Delta ADC = \Delta BCD\) nên AD = BC và BD = AC.
Hai tam giác ADB và BCA có:
AD = BC, BD = AC (theo chứng minh trên)
AB là cạnh chung
Vậy \(\Delta ADB = \Delta BCA\left( {c.c.c} \right)\)
Bài 7 trang 62 Vở thực hành Toán 7 thường xoay quanh các chủ đề về số nguyên, phép toán với số nguyên, và các bài toán ứng dụng liên quan đến số nguyên. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Để cung cấp lời giải chi tiết, chúng ta cần xem xét từng phần của bài tập. Thông thường, bài 7 trang 62 sẽ bao gồm một số câu hỏi nhỏ, yêu cầu học sinh thực hiện các phép toán hoặc giải quyết các bài toán ứng dụng. Dưới đây là một ví dụ minh họa:
Đề bài: Tính giá trị của biểu thức sau: a) (-5) + 8; b) 12 - (-3); c) (-4) x 5; d) (-20) : (-4)
Lời giải:
Ngoài các bài tập tính toán trực tiếp, bài 7 trang 62 còn có thể xuất hiện các dạng bài tập sau:
Để giải bài tập về số nguyên một cách nhanh chóng và chính xác, học sinh có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về số nguyên, học sinh nên luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các nguồn tài liệu học tập khác. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp các em tự tin hơn trong quá trình học tập.
Bài 7 trang 62 Vở thực hành Toán 7 là một bài tập quan trọng, giúp học sinh nắm vững kiến thức cơ bản về số nguyên và rèn luyện kỹ năng giải bài tập. Hy vọng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà Giaitoan.edu.vn cung cấp, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán.