Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 85, 86 Vở thực hành Toán 7 tập 2. Bài học này thuộc chương trình Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho tam giác ABC cân tại A, đường cao AH (left( {H in BC} right)). a) Chứng minh (Delta AHB = Delta AHC). b) Từ H kẻ đường thẳng song song với AC, cắt AB tại D. Chứng minh (AD = DH). c) Gọi M là trung điểm của AC, CD cắt AH tại G. Chứng minh ba điểm B, G, M thẳng hàng. d) Chứng minh chu vi (Delta ABC) lớn hơn (AH + 3BG).
Đề bài
Cho tam giác ABC cân tại A, đường cao AH \(\left( {H \in BC} \right)\).
a) Chứng minh \(\Delta AHB = \Delta AHC\).
b) Từ H kẻ đường thẳng song song với AC, cắt AB tại D. Chứng minh \(AD = DH\).
c) Gọi M là trung điểm của AC, CD cắt AH tại G. Chứng minh ba điểm B, G, M thẳng hàng.
d) Chứng minh chu vi \(\Delta ABC\) lớn hơn \(AH + 3BG\).
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta AHB = \Delta AHC\) (cạnh huyền – cạnh góc vuông)
b) Chứng minh \(\widehat {{A_1}} = \widehat {{A_2}}\), \(\widehat {{H_1}} = \widehat {{A_2}}\) suy ra \(\widehat {{A_1}} = \widehat {{H_1}}\) nên tam giác ADH cân tại D, suy ra \(AD = DH\).
c) Vì \(\widehat {{A_1}} + \widehat {ABC} = {90^o}\), \(\widehat {{H_1}} + \widehat {{H_2}} = \widehat {AHB} = {90^o}\), \(\widehat {{A_1}} = \widehat {{H_1}}\) nên \(\widehat {ABH} = \widehat {{H_2}}\) nên tam giác BHD cân tại D, suy ra \(BD = DH\). Mà \(AD = DH\) nên D là trung điểm của AB.
+ Chứng minh G là trọng tâm của tam giác ABC. Suy ra BG là trung tuyến, M là trung điểm của AC nên BG đi qua M, tức B, G, M thẳng hàng.
d) + Trên tia BM lấy điểm K sao cho M là trung điểm của BK, khi đó \(2BM = BK\).
+ Gọi G là trọng tâm của tam giác ABC nên \(3BG = 2BM\). Từ đó \(BK = 2BM = 3BG\).
+ Ta chứng minh được \(\Delta BMC = \Delta KMA\left( {c.g.c} \right)\), suy ra \(BC = AK\).
+ Chứng minh \(AK + AB > BK\) suy ra, \(BC + AB > 3BG\)
+ Chứng minh \(AC > AH\). Suy ra \(BC + AC + AB > AH + 3BG\).
Lời giải chi tiết
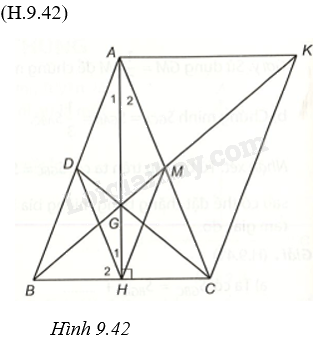
a) Xét hai tam giác vuông \(\Delta AHB\) và \(\Delta AHC\) có:
AH chung, \(AB = AC\)nên \(\Delta AHB = \Delta AHC\) (cạnh huyền – cạnh góc vuông).
b) Từ câu a) \(\Delta AHB = \Delta AHC\), suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng).
Ta có AC//HD, suy ra \(\widehat {{H_1}} = \widehat {{A_2}}\) (so le trong), từ đó \(\widehat {{A_1}} = \widehat {{H_1}}\) nên \(\Delta \)ADH cân tại D, suy ra \(AD = DH\). (1).
c) Ta có \(\widehat {{A_1}} + \widehat {ABC} = {90^o}\) (vì tam giác AHB vuông tại H), \(\widehat {{H_1}} + \widehat {{H_2}} = \widehat {AHB} = {90^o}\) (vì AH vuông góc với BC tại H). Vì \(\widehat {{A_1}} = \widehat {{H_1}}\) nên \(\widehat {ABH} = \widehat {{H_2}}\), suy ra tam giác BHD cân tại D, do đó \(BD = DH\). (2).
Từ (1) và (2) suy ra D là trung điểm của AB.
Tam giác ABC có CD, AH là hai trung tuyến cắt nhau tại G nên G là trọng tâm tam giác ABC.
Khi đó, BG là trung tuyến, M là trung điểm của AC nên BG đi qua M, tức B, G, M thẳng hàng.
d) Trên tia BM lấy điểm K sao cho M là trung điểm của BK, khi đó \(2BM = BK\).
Vì G là trọng tâm của tam giác ABC nên \(3BG = 2BM\). Từ đó \(BK = 2BM = 3BG\).
Ta chứng minh được \(\Delta BMC = \Delta KMA\left( {c.g.c} \right)\), suy ra \(BC = AK\).
Trong tam giác ABK, ta có:
\(AK + AB > BK\) hay \(BC + AB > BK\), mà \(BK = 2BM = 3BG\) nên \(BC + AB > 3BG\). (3)
Trong tam giác vuông AHC, ta có \(AC > AH\). (4)
Từ (3) và (4) suy ra \(BC + AC + AB > AH + 3BG\).
Bài 5 trong Vở thực hành Toán 7 tập 2 tập trung vào việc ôn tập và củng cố kiến thức về các phép toán với số hữu tỉ, đặc biệt là các phép cộng, trừ, nhân, chia. Các bài tập thường yêu cầu học sinh vận dụng các tính chất của phép toán để đơn giản hóa biểu thức hoặc tìm giá trị của biểu thức.
Bài 5 bao gồm các dạng bài tập sau:
Đề bài: Tính: a) 1/2 + 1/3; b) 2/5 - 1/4; c) 3/7 * 2/5; d) 4/9 : 1/3
Giải:
Đề bài: Tìm x: a) x + 1/2 = 3/4; b) x - 2/5 = 1/3
Giải:
Đề bài: Một cửa hàng có 20 kg gạo. Buổi sáng bán được 1/4 số gạo, buổi chiều bán được 1/5 số gạo còn lại. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Giải:
Số gạo bán được buổi sáng là: 20 * 1/4 = 5 kg
Số gạo còn lại sau buổi sáng là: 20 - 5 = 15 kg
Số gạo bán được buổi chiều là: 15 * 1/5 = 3 kg
Số gạo còn lại sau buổi chiều là: 15 - 3 = 12 kg
Vậy cửa hàng còn lại 12 kg gạo.
Ngoài Vở thực hành Toán 7 tập 2, các em có thể tham khảo thêm:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em sẽ học tập tốt môn Toán 7 và đạt kết quả cao trong các kỳ thi.