Chào mừng các em học sinh đến với lời giải chi tiết bài 3 (4.35) trang 79 Vở thực hành Toán 7. Bài học này thuộc chương trình Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán đại số cơ bản.
giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải dễ hiểu nhất.
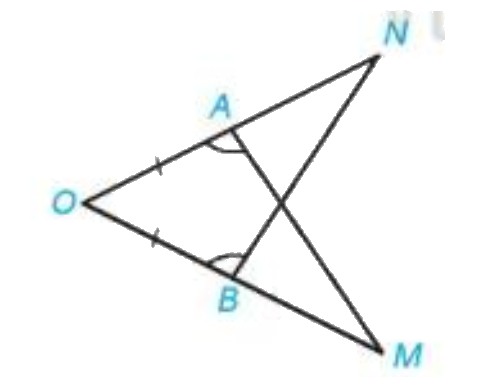
Bài 3 (4.35). Trong hình vẽ sau ta có AO = BO, \(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.
Đề bài
Bài 3 (4.35). Trong hình vẽ sau ta có AO = BO, \(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.
Phương pháp giải - Xem chi tiết
Chứng minh hai tam giác AOM và BON bằng nhau.
Lời giải chi tiết
Xét hai tam giác AOM và BON ta có:
\(\widehat {OAM} = \widehat {OBN}\), OA = OB (theo giả thiết)
\(\widehat {AOM} = \widehat {BON}\)(góc chung)
Vậy \(\Delta AOM = \Delta BON\)(g-c-g). Do đó AM = BN.
Bài 3 (4.35) trang 79 Vở thực hành Toán 7 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ, đặc biệt là phép cộng, trừ, nhân, chia. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các quy tắc và tính chất cơ bản của các phép toán này.
Đề bài yêu cầu thực hiện các phép tính sau:
Để giải bài tập này, chúng ta sẽ áp dụng các quy tắc sau:
a) (1/2 + 1/3) * 6/5
= (3/6 + 2/6) * 6/5
= 5/6 * 6/5
= 1
b) 3/4 - (1/2 + 1/4)
= 3/4 - (2/4 + 1/4)
= 3/4 - 3/4
= 0
c) 5/9 : (1/3 - 1/2)
= 5/9 : (2/6 - 3/6)
= 5/9 : (-1/6)
= 5/9 * (-6/1)
= -30/9 = -10/3
d) (1/2 - 1/3) : (1/4 + 1/6)
= (3/6 - 2/6) : (3/12 + 2/12)
= 1/6 : 5/12
= 1/6 * 12/5
= 12/30 = 2/5
Để tránh sai sót trong quá trình giải bài tập, các em cần:
Để rèn luyện thêm kỹ năng giải toán với số hữu tỉ, các em có thể tham khảo các bài tập tương tự sau:
Bài 3 (4.35) trang 79 Vở thực hành Toán 7 là một bài tập cơ bản nhưng quan trọng giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Bằng cách nắm vững các quy tắc và tính chất cơ bản, cùng với việc luyện tập thường xuyên, các em sẽ có thể giải bài tập này một cách dễ dàng và chính xác.