Bài 2 (10.21) trang 102 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 (10.21) trang 102 VTH Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tính thể tích, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lăng trụ trong Hình 10.21.
Đề bài
Tính thể tích, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lăng trụ trong Hình 10.21.
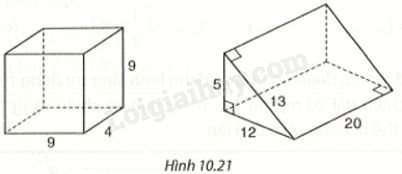
Phương pháp giải - Xem chi tiết
+ Thể tích hình hộp chữ nhật: \(V = a.b.c\) với a, b, c lần lượt là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật đó.
+ Thể tích của hình lăng trụ đứng tam giác: \(V = \) Sđáy.h, trong đó V là thể tích của hình lăng trụ đứng, Sđáy là diện tích một đáy của hình lăng trụ đứng, h là chiều cao của hình lăng trụ đứng.
+ Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: \({S_{xq}} = \) Cđáy.h, trong đó \({S_{xq}}\) là diện tích xung quanh của hình lăng trụ đứng, Cđáy là chu vi một đáy của hình lăng trụ đứng, h là chiều cao của hình lăng trụ đứng.
+ Diện tích xung quanh hình hộp chữ nhật: \({S_{xq}} = 2\left( {a + b} \right).c\) với a, b, c lần lượt là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật đó.
+ Diện tích toàn phần= diện tích xung quanh+ diện tích hai đáy.
Lời giải chi tiết
Diện tích xung quanh của hình hộp chữ nhật là: \({S_{xq}} = 2.\left( {9 + 4} \right).9 = 234\)
Diện tích toàn phần của hình hộp chữ nhật là: \({S_{tp}} = 234 + 2.9.4 = 306\)
Diện tích xung quanh của hình lăng trụ đứng tam giác là: \({S_{xq}} = \left( {5 + 12 + 13} \right).20 = 600\)
Diện tích toàn phần của hình lăng trụ đứng tam giác là: \({S_{tp}} = 600 + 2.\left( {\frac{1}{2}.5.12} \right) = 660\)
Bài 2 (10.21) trang 102 Vở thực hành Toán 7 tập 2 thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về biểu thức đại số và các phép toán số học. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc tính toán.
(Nội dung đề bài sẽ được chèn vào đây. Ví dụ: Tính giá trị của biểu thức: 3x + 2y khi x = 2 và y = -1)
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước thực hiện và kết quả cuối cùng. Ví dụ:)
Thay x = 2 và y = -1 vào biểu thức 3x + 2y, ta được:
3x + 2y = 3 * 2 + 2 * (-1) = 6 - 2 = 4
Vậy, giá trị của biểu thức 3x + 2y khi x = 2 và y = -1 là 4.
Để hiểu rõ hơn về phương pháp giải, chúng ta cùng xem xét một ví dụ khác:
(Ví dụ minh họa khác sẽ được trình bày ở đây, tương tự như lời giải chi tiết ở trên.)
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Bài 2 (10.21) trang 102 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán. Bằng cách nắm vững phương pháp giải và thực hành thường xuyên, các em sẽ tự tin hơn trong quá trình học tập môn Toán.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn giải bài 2 (10.21) trang 102 Vở thực hành Toán 7 tập 2 sẽ giúp các em học sinh học tập hiệu quả hơn. Chúc các em thành công!
| Biến | Giá trị |
|---|---|
| x | 2 |
| y | -1 |