Bài 4 trang 101 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học về tam giác cân, tam giác đều vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 101 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Quan sát Hình 10.20 và tìm giá trị của x, biết thể tích của hình lăng trụ là (15c{m^3}).
Đề bài
Quan sát Hình 10.20 và tìm giá trị của x, biết thể tích của hình lăng trụ là \(15c{m^3}\).
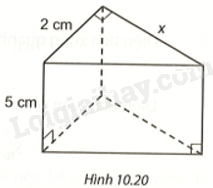
Phương pháp giải - Xem chi tiết
Thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: \(V = \) Sđáy.h, trong đó V là thể tích của hình lăng trụ đứng, Sđáy là diện tích một đáy của hình lăng trụ đứng, h là chiều cao của hình lăng trụ đứng.
Lời giải chi tiết
Diện tích đáy của lăng trụ là \(S = \frac{1}{2}.2.x = x\left( {c{m^2}} \right)\).
Hình lăng trụ có thể tích \(15c{m^3}\) nên ta có: \(x.5 = 15\) nên \(x = 15:5 = 3\left( {cm} \right)\).
Bài 4 trang 101 Vở thực hành Toán 7 tập 2 yêu cầu học sinh chứng minh một tính chất liên quan đến tam giác cân. Cụ thể, bài toán thường yêu cầu chứng minh nếu một tam giác có hai đường cao bằng nhau thì tam giác đó là tam giác cân. Để giải bài toán này, học sinh cần nắm vững các kiến thức về tam giác cân, tam giác đều, đường cao trong tam giác và các định lý liên quan.
Để giải bài 4 trang 101 Vở thực hành Toán 7 tập 2, chúng ta sẽ thực hiện theo các bước sau:
Dưới đây là lời giải chi tiết cho một dạng bài tập thường gặp trong bài 4 trang 101:
Lời giải:
Lời giải:
Ngoài các ví dụ trên, bài 4 trang 101 Vở thực hành Toán 7 tập 2 còn có nhiều dạng bài tập khác, như:
Để giải tốt các bài tập về tam giác cân, học sinh cần:
Để học tốt môn Toán 7, học sinh có thể tham khảo các tài liệu sau:
Bài 4 trang 101 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tam giác cân. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán 7.