Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 88, 89 Vở thực hành Toán 7 tập 2. Bài học này thuộc chương trình Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy hai điểm D và E sao cho (BD = CE). a) Chứng minh (Delta ADE) cân. b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của góc DAE và (AM bot DE). c) Từ B và C kẻ BH, CK theo thứ tự vuông góc với AD, AE. Chứng minh: (BH = CK). d) Chứng minh: HK//BC.
Đề bài
Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy hai điểm D và E sao cho \(BD = CE\).
a) Chứng minh \(\Delta ADE\) cân.
b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của góc DAE và \(AM \bot DE\).
c) Từ B và C kẻ BH, CK theo thứ tự vuông góc với AD, AE. Chứng minh: \(BH = CK\).
d) Chứng minh: HK//BC.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta ABD = \Delta ACE\) (c.g.c), do đó \(AD = AE\) nên tam giác ADE cân tại A.
b) + Chứng minh\(\Delta AMD = \Delta AME\) (c.c.c), suy ra \(\widehat {DAM} = \widehat {MAE}\) và \(\widehat {DMA} = \widehat {EMA}\), suy ra AM là phân giác của góc DAE.
+ Mặt khác do \(\widehat {DMA}\) và \(\widehat {AME}\) là hai góc bù nhau nên \(\widehat {DMA} = \widehat {AME} = {90^o}\) hay \(AM \bot DE\).
c) + Chứng minh\(\Delta ABH = \Delta ACK\) (cạnh huyền- góc nhọn), suy ra \(BH = CK\).
d) + Gọi giao điểm của AM và HK là N.
+ Chứng minh \(\Delta ANH = \Delta ANK\left( {c.g.c} \right)\), từ đó chứng minh được \(\widehat {ANH} = \widehat {ANK} = {90^o}\), suy ra \(AM \bot HK\)
+ Vì \(AM \bot HK\), mà \(AM \bot DE\) nên HK//BC.
Lời giải chi tiết
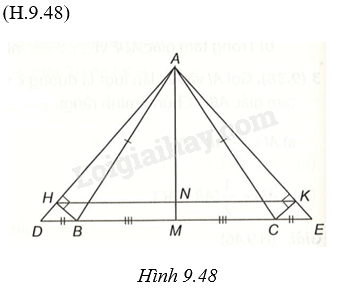
a) Do \(\Delta ABC\) cân tại A nên \(\widehat {ABC} = \widehat {ACB}\), suy ra \(\widehat {ABD} = \widehat {ACE}\) (cùng bù với góc ABC, ACB).
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(AB = AC\) (do tam giác ABC cân tại A), \(\widehat {ABD} = \widehat {ACE}\) (chứng minh trên), \(BD = CE\) (theo giả thiết), suy ra \(\Delta ABD = \Delta ACE\) (c.g.c), do đó \(AD = AE\) (hai cạnh tương ứng), suy ra \(\Delta ADE\) cân tại A.
b) Ta có: \(DM = DB + BM,EM = CE + MC\), mà \(BD = CE\) (gt), \(BM = MC\) (M là trung điểm của BC), suy ra \(DM = MC\).
Xét \(\Delta AMD\) và \(\Delta AME\) có:
AM chung, \(AD = AE\) (chứng minh trên), \(DM = MC\) (chứng minh trên)
Do đó \(\Delta AMD = \Delta AME\) (c.c.c), suy ra \(\widehat {DAM} = \widehat {MAE}\) và \(\widehat {DMA} = \widehat {EMA}\), suy ra AM là phân giác của góc DAE.
Mặt khác do \(\widehat {DMA}\) và \(\widehat {AME}\) là hai góc bù nhau nên \(\widehat {DMA} = \widehat {AME} = {90^o}\) \(AM \bot DE\).
c) Vì \(\Delta ABD = \Delta ACE\) (chứng minh trên) nên \(\widehat {DAB} = \widehat {CAE}\).
Xét tam giác vuông ABH và tam giác vuông ACK, ta có: \(\widehat {DAB} = \widehat {CAE},AB = AC\) nên \(\Delta ABH = \Delta ACK\) (cạnh huyền- góc nhọn), suy ra \(BH = CK\) (hai cạnh tương ứng).
d) Gọi giao điểm của AM và HK là N.
Xét \(\Delta ANH\) và \(\Delta ANK\), có: \(AH = AK\) (do \(\Delta ABH = \Delta ACK\)), \(\widehat {DAM} = \widehat {MAE}\) (chứng minh trên), AN là cạnh chung. Do đó, \(\Delta ANH = \Delta ANK\left( {c.g.c} \right)\), suy ra \(\widehat {ANH} = \widehat {ANK}\) (hai góc tương ứng), mà hai góc này kề bù nên \(\widehat {ANH} = \widehat {ANK} = {90^o}\), suy ra \(AM \bot HK\).
Ta có \(AM \bot HK\), mà \(AM \bot DE\) nên HK//BC.
Bài 5 trang 88, 89 Vở thực hành Toán 7 tập 2 thường xoay quanh các chủ đề về biểu thức đại số, các phép toán với biểu thức đại số, và việc rút gọn biểu thức. Để giải quyết các bài toán này một cách hiệu quả, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất giao hoán, kết hợp, phân phối của phép toán, và các quy tắc dấu ngoặc.
Trước khi đi vào giải bài tập cụ thể, chúng ta cần ôn lại một số khái niệm quan trọng:
Dưới đây là lời giải chi tiết cho từng phần của bài 5:
Đề bài: Rút gọn biểu thức: 3x + 2y - x + 5y
Lời giải:
Đề bài: Tính giá trị của biểu thức 2x - 3y khi x = 2 và y = -1
Lời giải:
Đề bài: Tìm x biết: 5x - 10 = 0
Lời giải:
Ngoài bài 5, Vở thực hành Toán 7 tập 2 còn nhiều bài tập tương tự. Để giải tốt các bài tập này, học sinh cần:
Kiến thức về biểu thức đại số và các phép toán với biểu thức đại số có ứng dụng rất lớn trong toán học và các lĩnh vực khác. Ví dụ, trong vật lý, biểu thức đại số được sử dụng để mô tả các định luật và công thức. Trong kinh tế, biểu thức đại số được sử dụng để phân tích và dự báo các xu hướng thị trường.
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 5 trang 88, 89 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về biểu thức đại số và các phép toán với biểu thức đại số. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em sẽ tự tin hơn trong việc giải các bài tập tương tự.