Chào mừng các em học sinh đến với lời giải chi tiết bài 2 (9.2) trang 67 Vở thực hành Toán 7 tập 2. Bài học này thuộc chương trình Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các biểu thức đại số và ứng dụng thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
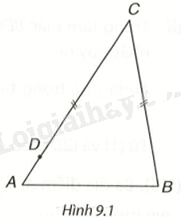
Trong Hình 9.1 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi kết luận nào trong các kết luận sau là đúng? Tại sao? a) (widehat A = widehat B). b) (widehat A > widehat B). c) (widehat A < widehat B).
Đề bài
Trong Hình 9.1 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi kết luận nào trong các kết luận sau là đúng? Tại sao?
a) \(\widehat A = \widehat B\).
b) \(\widehat A > \widehat B\).
c) \(\widehat A < \widehat B\).
Phương pháp giải - Xem chi tiết
Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
Lời giải chi tiết
Kết luận đúng là c. Bởi vì:
Ta có D nằm giữa A và C nên \(CD < CA\), mà \(CD = CB\), suy ra \(CB < CA\). Trong tam giác ABC, hai góc A và B lần lượt đối diện với cạnh BC và AC.
Theo định lí, góc đối diện với cạnh lớn hơn là góc lớn hơn nên \(\widehat A < \widehat B\).
Bài 2 (9.2) trang 67 Vở thực hành Toán 7 tập 2 yêu cầu học sinh vận dụng kiến thức về các phép toán với đa thức để thực hiện các phép tính đơn giản. Bài tập này giúp củng cố kỹ năng biến đổi biểu thức đại số, một nền tảng quan trọng cho các bài học nâng cao hơn.
Bài 2 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia đa thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc sau:
Yêu cầu: Thực hiện phép tính: (3x + 5y) + (2x - y)
Giải:
(3x + 5y) + (2x - y) = 3x + 5y + 2x - y = (3x + 2x) + (5y - y) = 5x + 4y
Yêu cầu: Thực hiện phép tính: (x2 - 2x + 1) - (x2 + x - 3)
Giải:
(x2 - 2x + 1) - (x2 + x - 3) = x2 - 2x + 1 - x2 - x + 3 = (x2 - x2) + (-2x - x) + (1 + 3) = -3x + 4
Yêu cầu: Thực hiện phép tính: 2x(x - 3) + 5x(x + 1)
Giải:
2x(x - 3) + 5x(x + 1) = 2x2 - 6x + 5x2 + 5x = (2x2 + 5x2) + (-6x + 5x) = 7x2 - x
Yêu cầu: Thực hiện phép tính: (x + 2)(x - 1)
Giải:
(x + 2)(x - 1) = x(x - 1) + 2(x - 1) = x2 - x + 2x - 2 = x2 + x - 2
Các kỹ năng giải bài tập về đa thức này có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học, đặc biệt là trong việc giải phương trình, bất phương trình và các bài toán về hàm số. Việc nắm vững các quy tắc và phương pháp giải bài tập này sẽ giúp học sinh tự tin hơn trong quá trình học tập.
Để rèn luyện thêm kỹ năng, các em có thể tự giải các bài tập tương tự sau:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên, các em học sinh đã hiểu rõ cách giải bài 2 (9.2) trang 67 Vở thực hành Toán 7 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!