Bài 4 (7.39) trang 50 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán số học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 (7.39) trang 50 Vở thực hành Toán 7 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Hãy cùng theo dõi lời giải chi tiết dưới đây!
Thực hiện các phép tính sau: a) (left( {{x^3} - 8} right):left( {x - 2} right)); b) (left( {x - 1} right)left( {x + 1} right)left( {{x^2} + 1} right)).
Đề bài
Thực hiện các phép tính sau:
a) \(\left( {{x^3} - 8} \right):\left( {x - 2} \right)\);
b) \(\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right)\).
Phương pháp giải - Xem chi tiết
a) Muốn chia một đa thức cho một đa thức, ta đặt tính và tiến hành chia (tương tự phép chia hai số tự nhiên) cho đến khi nhận được đa thức dư hoặc đa thức không, hoặc có bậc nhỏ hơn bậc của đa thức chia.
b) Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Lời giải chi tiết
a) Ta đặt tính như sau:
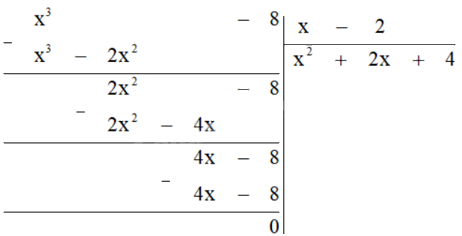
b) \(\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right) \)
\(= \left[ {\left( {x - 1} \right)\left( {x + 1} \right)} \right]\left( {{x^2} + 1} \right)\)
\( = \left[ {x\left( {x - 1} \right) + 1.\left( {x - 1} \right)} \right]\left( {{x^2} + 1} \right)\)
\( = \left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right)\)
\( = {x^4} - {x^2} + {x^2} - 1 = {x^4} - 1\)
Bài 4 (7.39) trang 50 Vở thực hành Toán 7 tập 2 thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng thực hiện các phép tính với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về cộng, trừ, nhân, chia số hữu tỉ, cũng như các tính chất của phép toán.
Đề bài thường yêu cầu thực hiện các phép tính với số hữu tỉ, có thể là các phép cộng, trừ, nhân, chia đơn giản, hoặc các phép tính phức tạp hơn kết hợp nhiều phép toán. Ví dụ:
Để giải bài tập này, học sinh cần thực hiện theo các bước sau:
a) (1/2) + (2/3)
Để cộng hai phân số này, ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 2 và 3 là 6.
(1/2) + (2/3) = (1*3)/(2*3) + (2*2)/(3*2) = (3/6) + (4/6) = (3+4)/6 = 7/6
b) (3/4) - (1/5)
Tương tự, ta quy đồng mẫu số của 4 và 5. Mẫu số chung nhỏ nhất của 4 và 5 là 20.
(3/4) - (1/5) = (3*5)/(4*5) - (1*4)/(5*4) = (15/20) - (4/20) = (15-4)/20 = 11/20
c) (2/7) * (5/9)
Để nhân hai phân số, ta nhân tử số với tử số, mẫu số với mẫu số.
(2/7) * (5/9) = (2*5)/(7*9) = 10/63
d) (4/11) : (2/3)
Để chia hai phân số, ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai.
(4/11) : (2/3) = (4/11) * (3/2) = (4*3)/(11*2) = 12/22 = 6/11
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, học sinh có thể luyện tập thêm các bài tập tương tự trong Vở thực hành Toán 7 tập 2, hoặc tìm kiếm các bài tập trực tuyến trên các trang web học toán.
Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi giải các bài tập toán học.
Bài 4 (7.39) trang 50 Vở thực hành Toán 7 tập 2 là một bài tập cơ bản về số hữu tỉ. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trên đây, các em học sinh sẽ hiểu rõ hơn về bài tập này và tự tin hơn trong quá trình học tập.