Bài 1 (9.10) trang 72 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ, đặc biệt là phép cộng, trừ, nhân, chia số hữu tỉ.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho các bộ ba đoạn thẳng có độ dài như sau: a) 2cm, 3cm, 5cm. b) 3cm, 4cm, 6cm. c) 2cm, 4cm, 5cm. Hỏi bộ ba nào không thể là độ dài ba cạnh của một tam giác? Vì sao? Với mỗi bộ ba còn lại, hãy vẽ một tam giác có độ dài ba cạnh được cho trong bộ ba đó.
Đề bài
Cho các bộ ba đoạn thẳng có độ dài như sau:
a) 2cm, 3cm, 5cm.
b) 3cm, 4cm, 6cm.
c) 2cm, 4cm, 5cm.
Hỏi bộ ba nào không thể là độ dài ba cạnh của một tam giác? Vì sao? Với mỗi bộ ba còn lại, hãy vẽ một tam giác có độ dài ba cạnh được cho trong bộ ba đó.
Phương pháp giải - Xem chi tiết
Để kiểm tra ba độ dài có là độ dài ba cạnh của một tam giác hay không, ta chỉ cần so sánh độ dài lớn nhất có nhỏ hơn tổng hai độ dài còn lại hoặc độ dài nhỏ nhất có lớn hơn hiệu hai độ dài còn lại hay không.
Lời giải chi tiết
a) Ta có \(2 + 3 = 5\) nên bộ ba đoạn thẳng có độ dài 2cm, 3cm, 5cm không thỏa mãn bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.
b) Ta có \(6 < 4 + 3\) nên bộ ba có độ dài 3cm, 4cm, 6cm thỏa mãn điều kiện trong Chú ý nêu ở trên nên là độ dài ba cạnh của một tam giác.
Ta dùng thước và compa vẽ được tam giác ABC có độ dài ba cạnh là 3cm, 4cm, 6cm như Hình 9.11.
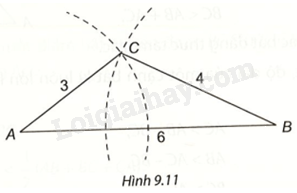
c) Ta có \(2 > 5 - 4\) nên ba độ dài 2cm, 4cm, 5cm thỏa mãn điều kiện trong Chú ý nêu ở trên nên là độ dài ba cạnh của một tam giác.
Ta dùng thước và compa vẽ được tam giác ABC có độ dài ba cạnh là 2cm, 4cm, 5cm như Hình 9.12.
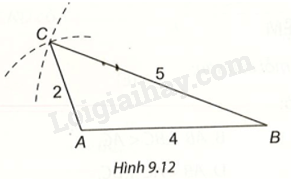
Bài 1 (9.10) trang 72 Vở thực hành Toán 7 tập 2 yêu cầu học sinh thực hiện các phép tính với số hữu tỉ. Để giải bài tập này, các em cần nắm vững các quy tắc về cộng, trừ, nhân, chia số hữu tỉ, cũng như quy tắc đổi dấu và rút gọn phân số.
Bài tập yêu cầu tính giá trị của các biểu thức sau:
a) (1/2) + (1/3)
Để cộng hai phân số, ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Ta có:
(1/2) + (1/3) = (3/6) + (2/6) = (3+2)/6 = 5/6
b) (2/5) - (1/4)
Tương tự, ta quy đồng mẫu số của 5 và 4. Mẫu số chung nhỏ nhất của 5 và 4 là 20. Ta có:
(2/5) - (1/4) = (8/20) - (5/20) = (8-5)/20 = 3/20
c) (3/4) * (2/7)
Để nhân hai phân số, ta nhân tử số với tử số và mẫu số với mẫu số. Ta có:
(3/4) * (2/7) = (3*2)/(4*7) = 6/28 = 3/14 (rút gọn)
d) (5/6) : (1/3)
Để chia hai phân số, ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai. Ta có:
(5/6) : (1/3) = (5/6) * (3/1) = (5*3)/(6*1) = 15/6 = 5/2
Khi thực hiện các phép tính với số hữu tỉ, các em cần chú ý đến quy tắc đổi dấu và rút gọn phân số để đảm bảo kết quả chính xác.
Ví dụ, nếu gặp biểu thức có dấu trừ trước dấu ngoặc, ta cần đổi dấu tất cả các số hạng trong ngoặc trước khi thực hiện phép tính.
Ngoài ra, sau khi thực hiện các phép tính, các em nên kiểm tra lại kết quả bằng cách sử dụng máy tính hoặc nhờ thầy cô giáo, bạn bè kiểm tra.
Để rèn luyện thêm kỹ năng giải bài tập về số hữu tỉ, các em có thể tham khảo các bài tập tương tự sau:
Bài 1 (9.10) trang 72 Vở thực hành Toán 7 tập 2 là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 7. Việc nắm vững các quy tắc về số hữu tỉ và thực hành giải nhiều bài tập tương tự sẽ giúp các em học sinh tự tin hơn trong việc giải các bài toán phức tạp hơn.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập này và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học!