Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 4 (9.4) trang 67, 68 trong Vở thực hành Toán 7 tập 2. Chúng tôi sẽ giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập, từ đó nâng cao kết quả học tập môn Toán.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu và bài giảng chất lượng cao dành cho học sinh cấp THCS.
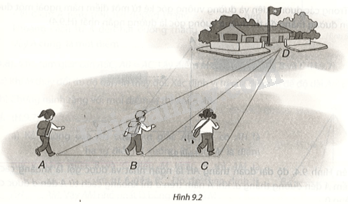
Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD và CD (H.9.2). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng, B nằm giữa A và C, (widehat {ACD}) là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?
Đề bài
Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD và CD (H.9.2). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng, B nằm giữa A và C, \(\widehat {ACD}\) là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?
Phương pháp giải - Xem chi tiết
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Lời giải chi tiết
Trong tam giác BDC có \(\widehat {ACD}\) là góc tù. Cạnh BD đối diện \(\widehat {ACD}\) nên BD là cạnh lớn nhất, suy ra \(BD > DC\). (1)
Tương tự, trong tam giác ABD có \(\widehat {ABD}\) là góc tù (vì \(\widehat {ABD}\) kề bù với góc nhọn \(\widehat {DBC}\)), cạnh AD đối diện với \(\widehat {ABD}\), suy ra \(AD > BD\). (2)
Từ (1) và (2), ta có \(AD > BD > DC\). Vậy bạn Mai đi xa nhất và bạn Hà đi gần nhất.
Bài 4 (9.4) trang 67, 68 Vở thực hành Toán 7 tập 2 thuộc chương trình học về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các loại góc (góc nhọn, góc tù, góc vuông, góc bẹt) và mối quan hệ giữa chúng để giải quyết các bài toán thực tế.
Bài 4 (9.4) thường bao gồm các dạng bài tập sau:
Bài 4.1: (Ví dụ) Cho hình vẽ, biết góc AOB = 60 độ. Tính số đo góc BOC.
Lời giải:
Vì góc AOB và góc BOC là hai góc kề bù nên:
AOB + BOC = 180 độ
60 độ + BOC = 180 độ
BOC = 180 độ - 60 độ = 120 độ
Vậy, số đo góc BOC là 120 độ.
Bài 4.2: (Ví dụ) Cho hai đường thẳng AB và CD cắt nhau tại O. Biết góc AOC = 50 độ. Tính số đo các góc còn lại.
Lời giải:
Vì góc AOC và góc BOD là hai góc đối đỉnh nên:
AOC = BOD = 50 độ
Vì góc AOC và góc COB là hai góc kề bù nên:
AOC + COB = 180 độ
50 độ + COB = 180 độ
COB = 180 độ - 50 độ = 130 độ
Vì góc COB và góc DOA là hai góc đối đỉnh nên:
COB = DOA = 130 độ
Vậy, số đo các góc còn lại là: BOD = 50 độ, COB = 130 độ, DOA = 130 độ.
Để nắm vững kiến thức về góc, bạn nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và vở bài tập. Ngoài ra, bạn có thể tham khảo các tài liệu học tập trực tuyến trên giaitoan.edu.vn.
Bài 4 (9.4) trang 67, 68 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về góc. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, bạn sẽ tự tin hơn khi giải quyết các bài toán tương tự.