Bài 5 (10.15) trang 99 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học về tam giác cân, tam giác đều vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 (10.15) trang 99 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
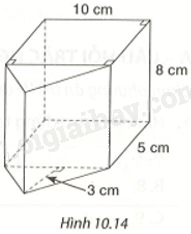
Một hình gồm hai hình lăng trụ đứng ghép lại với các kích thước như Hình 10.14. Tính thể tích của hình ghép.
Đề bài
Một hình gồm hai hình lăng trụ đứng ghép lại với các kích thước như Hình 10.14. Tính thể tích của hình ghép.
Phương pháp giải - Xem chi tiết
Thể tích hình ghép bằng tổng thể tích của hình hộp chữ nhật và hình lăng trụ đứng tam giác có độ dài đáy 10cm, chiều cao ứng với đáy là 3cm, chiều cao của hình lăng trụ đứng là 8cm.
Lời giải chi tiết
Thể tích hình lăng trụ đứng tam giác là: \({V_1} = \left( {\frac{1}{2}.3.10} \right).8 = 120\left( {c{m^3}} \right)\).
Thể tích hình hộp chữ nhật là: \({V_2} = 10.5.8 = 400\left( {c{m^3}} \right)\).
Thể tích của hình lăng trụ là: \(V = {V_1} + {V_2} = 120 + 400 = 520\left( {c{m^3}} \right)\).
Bài 5 (10.15) trang 99 Vở thực hành Toán 7 tập 2 thuộc chương trình học về tam giác cân và tam giác đều. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải bài tập thường bao gồm:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC. Chứng minh AD vuông góc với BC.)
Lời giải:
Vì tam giác ABC cân tại A và D là trung điểm của BC nên AD là đường trung tuyến đồng thời là đường cao của tam giác ABC.
Do đó, AD vuông góc với BC (điều phải chứng minh).
Để củng cố kiến thức về tam giác cân và tam giác đều, các em có thể tham khảo các bài tập tương tự sau:
Khi giải các bài tập này, các em cần chú ý:
Kiến thức về tam giác cân và tam giác đều có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như:
Bài 5 (10.15) trang 99 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tam giác cân và tam giác đều. Hy vọng với lời giải chi tiết và các hướng dẫn giải bài tập tương tự, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập Toán 7.