Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 71 Vở thực hành Toán 7. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
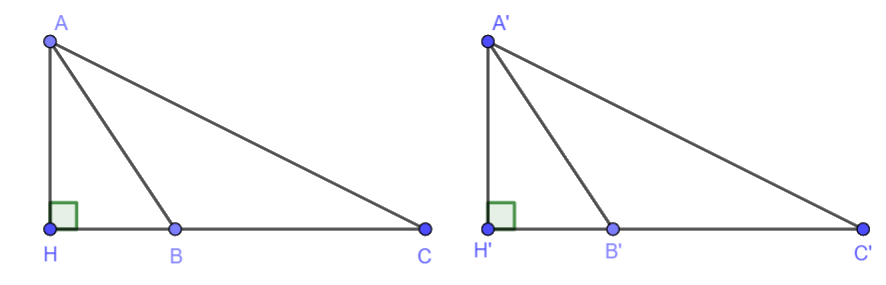
Bài 5. Cho hình vẽ dưới đây. Biết AB =A’B’, HB = H’B’, BC = B’C’. Chứng minh rằng AC = A’C’.
Đề bài
Bài 5. Cho hình vẽ dưới đây. Biết AB =A’B’, HB = H’B’, BC = B’C’.
Chứng minh rằng AC = A’C’.
Phương pháp giải - Xem chi tiết
Chứng minh hai tam giác AHC và A’H’C’ bằng nhau.
Lời giải chi tiết
Hai tam giác AHB và A’H’B’ lần lượt vuông tại đỉnh H, H’ và có:
AB = A’B’, HB = H’B’ (theo giả thiết)
Vậy \(\Delta AHB = \Delta A'H'B'\)(hai cạnh góc vuông). Do đó AH = A’H’.
Hai tam giác AHC và A’H’C’ lần lượt vuông tại đỉnh H, H’ và có:
AH = A’H’ (theo chứng minh trên)
HC = HB + BC = H’B’ + B’C’ = H’C’ (theo giả thiết)
Vậy \(\Delta AHC = \Delta A'H'C'\)(hai cạnh góc vuông). Do đó AC = A’C’.
Bài 5 trang 71 Vở thực hành Toán 7 thuộc chương trình học Toán lớp 7, thường liên quan đến các kiến thức về số nguyên, phép toán với số nguyên, hoặc các bài toán ứng dụng thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc tính toán liên quan.
Tùy thuộc vào từng bộ sách Vở thực hành Toán 7, nội dung bài 5 có thể khác nhau. Tuy nhiên, thường gặp các dạng bài tập sau:
Để giải bài 5 trang 71 Vở thực hành Toán 7, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Tính giá trị của biểu thức: (-3) + 5 - (-2) + 7
Giải:
(-3) + 5 - (-2) + 7 = -3 + 5 + 2 + 7 = 2 + 2 + 7 = 4 + 7 = 11
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tự giải các bài tập tương tự sau:
Bài 5 trang 71 Vở thực hành Toán 7 là một bài tập quan trọng giúp học sinh củng cố kiến thức về số nguyên và rèn luyện kỹ năng giải bài tập. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ tự tin giải bài tập một cách hiệu quả.
| Dạng bài tập | Phương pháp giải |
|---|---|
| Tính toán với số nguyên | Áp dụng quy tắc cộng, trừ, nhân, chia số nguyên |
| Tìm số | Sử dụng các phép toán để tìm số thỏa mãn điều kiện |
| Ứng dụng thực tế | Phân tích bài toán, lập phương trình và giải phương trình |