Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 57 Vở thực hành Toán 7. Bài học này thuộc chương trình Toán 7 tập 1, tập trung vào việc vận dụng các kiến thức về số nguyên, phép toán trên số nguyên để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Bài 6. Tính các số đo x, y, z của các góc trong hình vẽ dưới đây
Đề bài
Bài 6. Tính các số đo x, y, z của các góc trong hình vẽ dưới đây
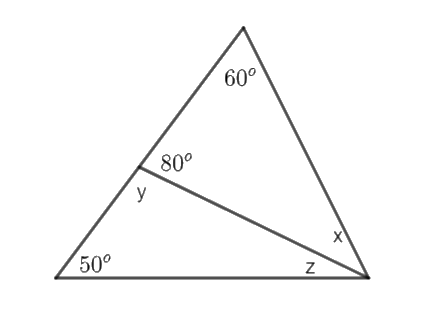
Phương pháp giải - Xem chi tiết
Tổng ba góc trong một tam giác bằng \({180^o}\) và tổng hai góc kề bù bằng \({180^o}\).
Lời giải chi tiết
Vì x, \({80^o}\), \({60^o}\) là số đo ba góc trong một tam giác nên chúng có tổng bằng \({180^o}\). Do đó ta có:
\({80^o} + x + {60^o} = {180^o} \Rightarrow x = {180^o} - {60^o} - {80^o} = {40^o}\)
Do y, \({80^o}\)nên chúng có tổng bằng \({180^o}\). Do đó ta có:
\({80^o} + y = {180^o} \Rightarrow y = {180^o} - {80^o} = {100^o}\)
Tương tự vì y, z, \({50^o}\) là số đo ba góc trong một tam giác nên chúng có tổng bằng \({180^o}\). Do đó ta có:
\(y + z + {50^o} = {180^o} \Rightarrow z = {180^o} - {50^o} - y = {30^o}\)
Kết luận \(x = {40^o},y = {100^o},z = {30^o}\)
Bài 6 trang 57 Vở thực hành Toán 7 thường xoay quanh các bài toán liên quan đến số nguyên, các phép cộng, trừ, nhân, chia số nguyên, và các tính chất của phép toán. Mục tiêu chính của bài tập là giúp học sinh củng cố kiến thức về số nguyên, rèn luyện kỹ năng tính toán, và áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Để giải quyết bài 6 trang 57 Vở thực hành Toán 7 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Bài 6 thường bao gồm nhiều câu hỏi nhỏ, mỗi câu hỏi yêu cầu học sinh thực hiện một phép toán hoặc giải một bài toán cụ thể. Dưới đây là hướng dẫn giải chi tiết từng phần của bài 6:
Để tính giá trị của một biểu thức, chúng ta cần thực hiện các phép toán theo đúng thứ tự: trong ngoặc trước, sau đó đến phép nhân, chia, cuối cùng là phép cộng, trừ.
Ví dụ: Tính giá trị của biểu thức 2 + 3 * 4.
Để tìm x trong một phương trình, chúng ta cần thực hiện các phép toán để đưa x về một vế và các số hạng còn lại về vế kia. Sau đó, chúng ta có thể tìm được giá trị của x.
Ví dụ: Tìm x biết x + 5 = 10.
Để giải một bài toán thực tế, chúng ta cần đọc kỹ đề bài, xác định các dữ kiện và yêu cầu của bài toán. Sau đó, chúng ta cần xây dựng một phương trình hoặc một biểu thức toán học để mô tả bài toán. Cuối cùng, chúng ta cần giải phương trình hoặc tính giá trị của biểu thức để tìm ra đáp án.
Trong bài 6 trang 57 Vở thực hành Toán 7, học sinh có thể gặp các dạng bài tập sau:
Để giải bài tập Toán 7 hiệu quả, học sinh có thể áp dụng các mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể làm thêm các bài tập tương tự sau:
Bài 6 trang 57 Vở thực hành Toán 7 là một bài tập quan trọng giúp học sinh củng cố kiến thức về số nguyên và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin giải quyết bài tập một cách nhanh chóng và chính xác.