Bài 6 trang 79 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ, đặc biệt là các phép cộng, trừ, nhân, chia.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu bài 6 trang 79 Vở thực hành Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC vuông tại A có góc B bằng ({60^o}). Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC (left( {M in BC} right)). a) Chứng minh (Delta ABE = Delta MBE). b) Chứng minh (MB = MC). c) Gọi I là giao điểm của BA và ME. Chứng minh (IE > EM).
Đề bài
Cho tam giác ABC vuông tại A có góc B bằng \({60^o}\). Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC \(\left( {M \in BC} \right)\).
a) Chứng minh \(\Delta ABE = \Delta MBE\).
b) Chứng minh \(MB = MC\).
c) Gọi I là giao điểm của BA và ME. Chứng minh \(IE > EM\).
Phương pháp giải - Xem chi tiết
a) Chỉ ra \(\widehat {BAE} = \widehat {BME} = {90^o},\widehat {ABE} = \widehat {EBM},BE\;chung\) nên \(\Delta ABE = \Delta MBE\).
b) Chứng minh \(\widehat {EBC} = \widehat C = {30^o}\) nên tam giác BEC cân tại E, suy ra EM là đường cao đồng thời là đường trung tuyến, suy ra \(MB = MC\).
c) + Chứng minh tam giác AEI vuông tại A nên \(IE > AE\)
+ Vì \(\Delta ABE = \Delta MBE\) nên \(AE = EM\). Do đó, \(IE > EM\).
Lời giải chi tiết
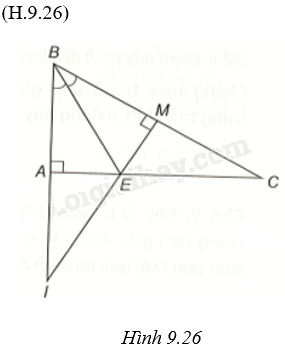
a) Xét hai tam giác vuông ABE và MBE, ta có:
\(\widehat {BAE} = \widehat {BME} = {90^o},\widehat {ABE} = \widehat {EBM},BE\;chung\)
Do đó, \(\Delta ABE = \Delta MBE\) (cạnh huyền – góc nhọn)
b) Trong tam giác vuông ABC, ta có \(\widehat B = {60^o}\) nên \(\widehat C = {30^o}\).
Vì BE là phân giác của \(\widehat {ABC}\) nên \(\widehat {ABE} = \widehat {EBM} = \frac{{\widehat {ABC}}}{2} = {30^o}\)
Vậy tam giác BEC có \(\widehat {EBC} = \widehat C = {30^o}\) nên tam giác BEC cân tại E.
Tam giác BEC cân tại E và có EM là đường cao đồng thời là đường trung tuyến, suy ra \(MB = MC\).
c) Ta có góc BAE kề bù với góc IAE nên \(\widehat {IAE} = {90^o}\).
Trong tam giác vuông AEI có cạnh IE là cạnh huyền nên \(IE > AE\) (1)
Theo câu a) \(\Delta ABE = \Delta MBE\) nên \(AE = EM\) (2)
Từ (1) và (2) suy ra \(IE > EM\).
Bài 6 trang 79 Vở thực hành Toán 7 tập 2 thuộc chương trình học về số hữu tỉ. Bài tập này yêu cầu học sinh vận dụng các quy tắc cộng, trừ, nhân, chia số hữu tỉ để tính toán và rút gọn biểu thức. Việc nắm vững các quy tắc này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 6 trang 79 Vở thực hành Toán 7 tập 2 thường bao gồm các dạng bài tập sau:
Để giải bài 6 trang 79 Vở thực hành Toán 7 tập 2 hiệu quả, học sinh cần:
Dưới đây là lời giải chi tiết cho từng phần của bài 6 trang 79 Vở thực hành Toán 7 tập 2. (Lưu ý: Nội dung cụ thể của bài tập sẽ thay đổi tùy theo từng phiên bản Vở thực hành)
Cho biểu thức: A = (1/2) + (2/3) - (3/4). Hãy tính giá trị của A.
Giải:
Để tính giá trị của A, ta cần quy đồng mẫu số của các phân số. Mẫu số chung nhỏ nhất của 2, 3 và 4 là 12.
A = (6/12) + (8/12) - (9/12) = (6 + 8 - 9)/12 = 5/12
Vậy, giá trị của biểu thức A là 5/12.
Cho biểu thức: B = (2/5) * (3/7) + (1/5) * (3/7). Hãy rút gọn biểu thức B.
Giải:
Ta có thể sử dụng tính chất phân phối để rút gọn biểu thức B.
B = (3/7) * ((2/5) + (1/5)) = (3/7) * (3/5) = 9/35
Vậy, biểu thức B được rút gọn là 9/35.
Một cửa hàng có 200 kg gạo. Ngày đầu bán được 1/4 số gạo, ngày thứ hai bán được 2/5 số gạo còn lại. Hỏi sau hai ngày, cửa hàng còn lại bao nhiêu kg gạo?
Giải:
Số gạo bán được trong ngày đầu là: 200 * (1/4) = 50 kg
Số gạo còn lại sau ngày đầu là: 200 - 50 = 150 kg
Số gạo bán được trong ngày thứ hai là: 150 * (2/5) = 60 kg
Số gạo còn lại sau hai ngày là: 150 - 60 = 90 kg
Vậy, sau hai ngày, cửa hàng còn lại 90 kg gạo.
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, học sinh có thể luyện tập thêm các bài tập tương tự trong Vở thực hành Toán 7 tập 2 và các tài liệu tham khảo khác.
Bài 6 trang 79 Vở thực hành Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ. Bằng cách nắm vững các quy tắc và phương pháp giải, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.