Chào mừng các em học sinh đến với lời giải chi tiết bài 9 Vở thực hành Toán 7 tập 2. Bài học này tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng áp dụng công thức.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho tam giác ABC cân tại đỉnh A. Gọi H là trung điểm của BC. a) Chứng minh (AH bot BC). b) Trên tia đối của tia BC lấy điểm M; trên tia đối của tia CB lấy điểm N sao cho (BM = CN). Chứng minh rằng (Delta ABM = Delta ACN). c) Gọi I là điểm trên AM, K là điểm trên AN sao cho (BI bot AM;CK bot AN). Chứng minh rằng tam giác AIK cân tại A, từ đó suy ra IK//MN.
Đề bài
Cho tam giác ABC cân tại đỉnh A. Gọi H là trung điểm của BC.
a) Chứng minh \(AH \bot BC\).
b) Trên tia đối của tia BC lấy điểm M; trên tia đối của tia CB lấy điểm N sao cho \(BM = CN\). Chứng minh rằng \(\Delta ABM = \Delta ACN\).
c) Gọi I là điểm trên AM, K là điểm trên AN sao cho \(BI \bot AM;CK \bot AN\). Chứng minh rằng tam giác AIK cân tại A, từ đó suy ra IK//MN.
Phương pháp giải - Xem chi tiết
a) Tam giác ABC cân tại A nên AH là đường trung tuyến đồng thời là đường cao.
b) + Vì \(\widehat {ABM} + \widehat {ABC} = {180^o}\), \(\widehat {ACN} + \widehat {ACB} = {180^o}\), \(\widehat {ABC} = \widehat {ACB}\) nên \(\widehat {ABM} = \widehat {ACN}\).
+ Chứng minh \(\Delta ABM = \Delta ACN\) (c.g.c).
c) + \(\Delta BIM = \Delta CKN\) (cạnh huyền – góc nhọn) nên \(MI = NK\). Mà \(AM = AN\) nên \(AI = AK\), suy ra \(\Delta AIK\) cân tại A. Suy ra \(\widehat {AIK} = \frac{{{{180}^o} - \widehat {IAK}}}{2}\).
+ Chứng minh \(\Delta AMN\) cân tại A nên \(\widehat {AMN} = \frac{{{{180}^o} - \widehat {MAN}}}{2}\). Suy ra \(\widehat {AIK} = \widehat {AMN}\) suy ra IK//MN.
Lời giải chi tiết
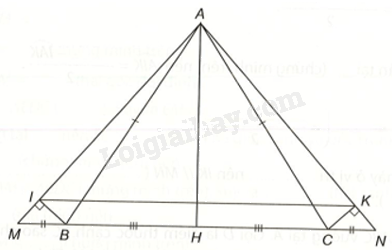
a) \(\Delta \)ABC cân tại A (giả thiết)
Mà AH là đường trung tuyến (H là trung điểm của BC)
Nên AH là đường cao của \(\Delta ABC\) (tính chất tam giác cân).
Vậy \(AH \bot BC\).
b) Ta có: \(\widehat {ABM} + \widehat {ABC} = {180^o}\) (hai góc kề bù), \(\widehat {ACN} + \widehat {ACB} = {180^o}\) (hai góc kề bù).
Mà \(\widehat {ABC} = \widehat {ACB}\) nên \(\widehat {ABM} = \widehat {ACN}\)
\(\Delta ABM\) và \(\Delta ACN\) có:
\(AB = AC\) (\(\Delta ABC\) cân tại đỉnh A).
\(\widehat {ABM} = \widehat {ACN}\) (chứng minh trên)
\(BM = CN\) (giả thiết)
Nên \(\Delta ABM = \Delta ACN\) (c.g.c).
c) Ta có \(\Delta ABM = \Delta ACN\) (chứng minh trên) suy ra \(\widehat {BMI} = \widehat {CNK}\) (hai góc tương ứng) và \(AM = AN\) (hai cạnh tương ứng).
\(\Delta BIM\left( {\widehat {BIM} = {{90}^o}} \right)\) và \(\Delta CKN\left( {\widehat {CKN} = {{90}^o}} \right)\) có:
\(BM = CN\) (giả thiết)
\(\widehat {BMI} = \widehat {CNK}\) (chứng minh trên)
Nên \(\Delta BIM = \Delta CKN\) (cạnh huyền – góc nhọn).
Suy ra \(MI = NK\) (hai cạnh tương ứng).
Mà \(AM = AN\) (chứng minh trên) nên \(AI = AK\), suy ra \(\Delta AIK\) cân tại A (dấu hiệu nhận biết tam giác cân).
Ta có \(AM = AN\)(chứng minh trên) nên \(\Delta AMN\) cân tại A (dấu hiệu nhận biết tam giác cân).
Suy ra \(\widehat {AMN} = \frac{{{{180}^o} - \widehat {MAN}}}{2}\).
Ta có \(\Delta AIK\) cân tại A (chứng minh trên) nên \(\widehat {AIK} = \frac{{{{180}^o} - \widehat {IAK}}}{2}\).
Từ đó \(\widehat {AIK} = \widehat {AMN}\left( { = \frac{{{{180}^o} - \widehat {IAK}}}{2}} \right)\)
Mà hai góc này ở vị trí đồng vị nên IK//MN (dấu hiệu nhận biết hai đường thẳng song song).
Bài 9 Vở thực hành Toán 7 tập 2 thuộc chương trình học Toán 7, tập trung vào việc ôn tập và củng cố kiến thức về các phép toán với số hữu tỉ, tỉ số, phần trăm và ứng dụng vào giải quyết các bài toán thực tế. Để giải quyết bài tập trong bài này, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc tính toán đã được học.
Bài 9 Vở thực hành Toán 7 tập 2 bao gồm các dạng bài tập sau:
Để giải bài tập trong bài 9 Vở thực hành Toán 7 tập 2 một cách hiệu quả, học sinh nên thực hiện theo các bước sau:
Bài 9.1: Tính giá trị của biểu thức sau: (1/2 + 1/3) * 6/5
Giải:
(1/2 + 1/3) * 6/5 = (3/6 + 2/6) * 6/5 = 5/6 * 6/5 = 1
Bài 9.2: Một cửa hàng bán một chiếc áo với giá gốc là 200.000 đồng. Sau khi giảm giá 10%, cửa hàng bán chiếc áo với giá bao nhiêu?
Giải:
Số tiền giảm giá là: 200.000 * 10% = 20.000 đồng
Giá bán sau khi giảm giá là: 200.000 - 20.000 = 180.000 đồng
Bài 9.3: So sánh hai số hữu tỉ: -3/4 và 2/5
Giải:
-3/4 = -0.75 và 2/5 = 0.4
Vì -0.75 < 0.4 nên -3/4 < 2/5
Bài 9.4: Tìm giá trị của x trong phương trình: x + 2/3 = 5/6
Giải:
x = 5/6 - 2/3 = 5/6 - 4/6 = 1/6
Bài 9.5: Một lớp học có 30 học sinh, trong đó có 12 học sinh giỏi. Tính tỉ lệ phần trăm học sinh giỏi của lớp.
Giải:
Tỉ lệ phần trăm học sinh giỏi là: (12/30) * 100% = 40%
Bài 9.6: Một người mua 5 kg gạo với giá 15.000 đồng/kg. Hỏi người đó phải trả bao nhiêu tiền?
Giải:
Tổng số tiền người đó phải trả là: 5 * 15.000 = 75.000 đồng
Trong quá trình giải bài tập, học sinh cần chú ý các điểm sau:
Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả này, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài tập Toán 7. Chúc các em học tốt!